
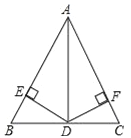
【题目】如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
(1)求证:AB=AC;
(2)若AD=![]() ,∠DAC=30°,求AC的长.
,∠DAC=30°,求AC的长.
【答案】(1)证明见解析;(2)4.
【解析】
试题分析:(1)先证明△DEB≌△DFC得∠B=∠C由此即可证明.
(2)先证明AD⊥BC,再在RT△ADC中,利用30°角性质设CD=a,AC=2a,根据勾股定理列出方程即可解决问题.
试题解析:(1)证明:∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,∴DE=DF,∠DEB=∠DFC=90°,在RT△DEB和RT△DFC中,∵BD=DC,DE=DF,∴△DEB≌△DFC,∴∠B=∠C,∴AB=AC.
(2)∵AB=AC,BD=DC,∴AD⊥BC,在RT△ADC中,∵∠ADC=90°,AD=![]() ,∠DAC=30°,∴AC=2CD,设CD=a,则AC=2a,∵
,∠DAC=30°,∴AC=2CD,设CD=a,则AC=2a,∵![]() ,∴
,∴![]() ,∵a>0,∴a=2,∴AC=2a=4.
,∵a>0,∴a=2,∴AC=2a=4.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E且AB=6cm,则△DEB的周长为( )cm. 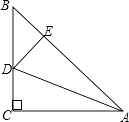
A.6
B.8
C.10
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30﹣40含起点值30,不含终点值40),得到其频数及频率如表:
数据段 | 频数 | 频率 |
30﹣40 | 10 | 0.05 |
40﹣50 | 36 | c |
50﹣60 | a | 0.39 |
60﹣70 | b | d |
70﹣80 | 20 | 0.10 |
总计 | 200 | 1 |
(1)表中a、b、c、d分别为:a=; b=; c=; d= .
(2)补全频数分布直方图;
(3)如果某天该路段约有1500辆通过,汽车时速不低于60千米即为违章,通过该统计数据估计当天违章车辆约有多少辆? 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是确定事件的是( )
A、阴天一定会下雨
B、黑暗中从5把不同的钥匙中随意摸出一把,用它打开了门
C、打开电视机,任选一个频道,屏幕上正在播放新闻联播
D、在五个抽屉中任意放入6本书,则至少有一个抽屉里有两本书
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图1,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图3,四边形ABCD中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC= (用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2+2x-5=0,此方程可变形为( )
A.(x-1)2=6B.(x+1)2=6C.(x+1)2=4D.(x-1)2=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P(1,1),N(2,0),△MNP和△M1N1P1的顶点都在格点上,△MNP与△M1N1P1是关于某一点中心对称,则对称中心的坐标为 .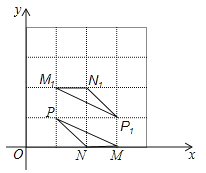
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com