
分析 (1)根据售价为每件60元,可赚20元钱,可知进价为40元,根据每件涨价1元,每星期要少卖出10件,可知每件涨价3元,小聪的妈妈每星期卖出300-30=270件;
(2)依题意,利润=单件利润×销售量,可得y与x的函数关系式;
(3)不能.把函数关系式用配方法化为-10(x-5)2+6250,y有最大值为6250.
(4)令-10x2+100x+6000=0,求出抛物线与x轴的交点,运用二次函数的图象和性质可知获利时x的取值范围.
解答 解:(1)根据售价为每件60元,可赚20元钱,可知进价=60-20=40元,根据每件涨价1元;每星期要少卖出10件,可知每件涨价3元,小聪的妈妈每星期卖出300-30=270件;
故答案为:40,270件.
(2)y=(20+x)(300-10x)=-10x2+100x+6000;
(3)每月该商场销售该种商品获利不能达到7000元,理由如下:
∵y=-10x2+100x+6000=-10(x-5)2+6250,
当x=5时,y取最大值为6250元,小于7000元,
∴不能达到;
(3)不是
依题意有:-10x2+100x+6000=0,
解得:x1=-20,x2=30,
∵-10<0,
∴当-20<x<30时,y>0,
即售价在40元到90元之间,小聪的妈妈就可获利,
∵x=-$\frac{b}{2a}$=-$\frac{100}{2×(-10)}$=5,
即涨价5元,售价为65元时,利润最大,并不是售价越高获利越大.
点评 本题考查的是二次函数的实际应用,把实际问题转化为数学问题,熟练运用二次函数的图象和性质是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲队 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙队 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
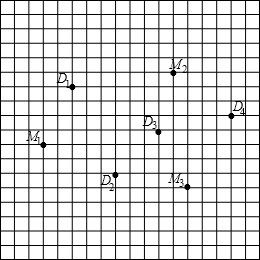 如图,某小区有大米产品加工点3个(M1,M2,M3),大豆产品加工点4个(D1,D2,D3,D4),为了加强食品安全监督,政府要求对食品加工点进行网格化管理,管理员绘制了坐标网格和建立了平面直角坐标系(隐藏),把图中的大米加工点用坐标表示为M1(-5,-1),M2(4,4),M3(5,-4).
如图,某小区有大米产品加工点3个(M1,M2,M3),大豆产品加工点4个(D1,D2,D3,D4),为了加强食品安全监督,政府要求对食品加工点进行网格化管理,管理员绘制了坐标网格和建立了平面直角坐标系(隐藏),把图中的大米加工点用坐标表示为M1(-5,-1),M2(4,4),M3(5,-4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}x(x-1)=90$ | B. | $\frac{1}{2}x(x+1)=90$ | C. | x(x-1)=90 | D. | x(x+1)=90 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
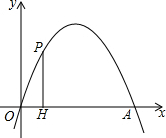 如图,抛物线y=-x2+mx过点A(4,0),O位坐标原点,设点P是x轴上方抛物线上的一个动点,过点P作PH⊥x轴,H为垂足,则PH+HO最大值为$\frac{25}{4}$.
如图,抛物线y=-x2+mx过点A(4,0),O位坐标原点,设点P是x轴上方抛物线上的一个动点,过点P作PH⊥x轴,H为垂足,则PH+HO最大值为$\frac{25}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 直线a向上平移1个单位得到直线b | B. | 直线a向下平移1个单位得到直线b | ||
| C. | 直线a向左平移1个单位得到直线b | D. | 直线a向右平移1个单位得到直线b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com