
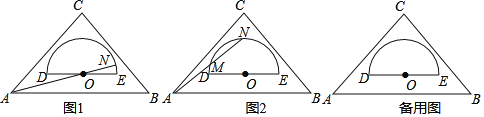
【题目】如图1是一块内置量角器的等腰直角三角板,它是一个轴对称图形.已知量角器所在的半圆O的直径DE与AB之间的距离为1,DE=4,AB=8,点N为半圆O上的一个动点,连结AN交半圆或直径DE于点M.
(1)当AN经过圆心O时,求AN的长;
(2)如图2,若N为量角器上表示刻度为90°的点,求△MON的周长;
(3)当![]() 时,求△MON的面积.
时,求△MON的面积.
【答案】(1)AN=![]() +2;(2)
+2;(2)![]() ;(3)
;(3)![]() 或1﹣
或1﹣![]() .
.
【解析】
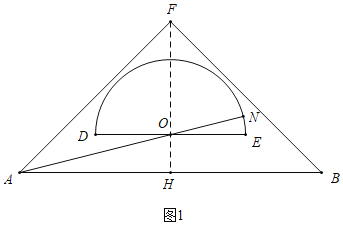
(1)如图1中,连接FO延长FO交AB于H.则FH⊥AB,FH⊥DE.解直角三角形求出AO即可解决问题.
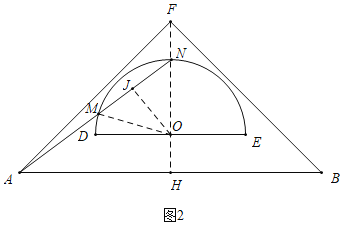
(2)如图2中,连接OM,作OJ⊥MN.利用相似三角形的性质求出NJ,再利用垂径定理求出MN即可解决问题.
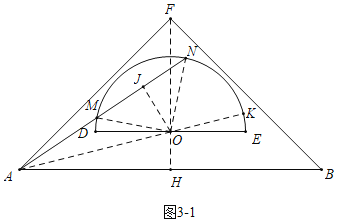
(3)分两种情形:如图3﹣1中,连接AO,延长AO交⊙O于K,作OJ⊥MN于J,连接OM,ON.设AM=MN=x,OJ=y,构建方程组即可解决问题.如图3﹣2中,连接ON,作NJ⊥AB于J交DE于K.想办法求出OM,NK即可解决问题.
(1)如图1中,连接FO延长FO交AB于H.则FH⊥AB,FH⊥DE.
∵DE=4,
∴⊙O的半径为2,
∵FA=FB,FH⊥AB,
∴AH=HB=4,
在![]() 中,OH=1,AH=4,
中,OH=1,AH=4,
∴![]() ,
,
∴![]() ;
;
(2)如图2中,连接OM,作OJ⊥MN于J.
在![]() 中, AH=4,
中, AH=4,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() 公共,
公共,
∴△OJN∽△AHN,
∴![]() ,即
,即![]() ,
,
∴JN=![]() ,
,
∵OJ⊥MN,OM=ON,
∴JM=JN,
∴MN=2JN=![]() ,
,
∴△MON的周长=2+2+![]() =
=![]() ;
;
(3)如图3﹣1中,连接AO并延长AO交⊙O于K,作OJ⊥MN于J,连接OM,ON.
∵![]() ,
,
∴AM=MN=![]() ,
,
设AM=MN=x,OJ=y,
∵OJ⊥MN,OM=ON,
∴JM=JN=![]() ,
,
在![]() 中,
中,
![]() ,即
,即![]() ①,
①,
在![]() 中, AO=
中, AO=![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ②,
②,
联立①②并解得![]() ,
,![]() ,
,
∴![]() ,OJ=
,OJ=![]() ,
,
∴S△MON=![]() .
.
如图3﹣2中,连接ON,作NJ⊥AB于J交DE于K.
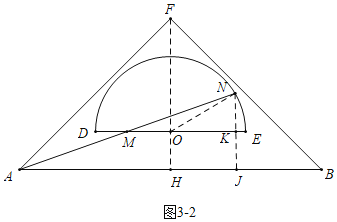
∵AM=MN,MK∥AJ,
∴MK是![]() 的中位线,
的中位线,
∴NK=JK=OH=1,MK=![]() AJ,
AJ,
∵NJ⊥AB,DE∥AB,
∴NK⊥OE,
∴sin∠NOK=![]() ,
,
∵![]() ,
,
∴∠NOK=![]() ,
,
∴OK=![]() NK=
NK=![]() ,
,
∵NJ⊥AB,FH⊥AB,DE∥AB,
∴四边形OKJH是矩形,
∴HJ=OK=![]() ,
,
∴AJ= AH+ HJ =4+![]() ,
,
∴MK=![]() AJ=2+
AJ=2+![]() ,
,
∴OM=MK﹣OK= 2+![]() ﹣
﹣![]() =2﹣
=2﹣![]() ,
,
∴S△MON=![]() (2﹣
(2﹣![]() )×1=1﹣
)×1=1﹣![]() ,
,
综上所述,满足条件的△MON的面积为![]() 或1﹣
或1﹣![]() .
.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)如图所示,下列结论中:
①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1).
其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
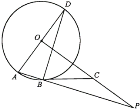
【题目】如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P,过B点的切线交OP于点C.
(1)求证:∠CBP=∠ADB.
(2)若OA=2,AB=1,求线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象分别交x轴、y轴于C,D两点,交反比例函数
的图象分别交x轴、y轴于C,D两点,交反比例函数![]() 图象于A(
图象于A(![]() ,4),B(3,m)两点.
,4),B(3,m)两点.
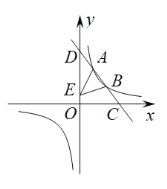
(1)求直线CD的表达式;
(2)点E是线段OD上一点,若![]() ,求E点的坐标;
,求E点的坐标;
(3)请你根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
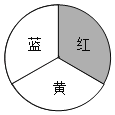
【题目】某商场开业,为了活跃气氛,用红、黄、蓝三色均分的转盘设计了两种抽奖方案,凡来商场消费的顾客都可以选择一种抽奖方案进行抽奖.
方案一:转动转盘一次,指针落在红色区域可领取一份奖品;
方案二:转动转盘两次,指针落在不同颜色区域可领取一份奖品,你会选择哪个方案?请用相关的数学知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,抛物线的对称轴x=1,与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的解析式及A、B点的坐标.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形;若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大;求出此时P点的坐标和四边形ABPC的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=13,BE=4,点F从点B出发,在折线段BA﹣AD上运动,连接EF,当EF⊥BC时停止运动,过点E作EG⊥EF,交矩形的边于点G,连接FG.设点F运动的路程为x,△EFG的面积为S.
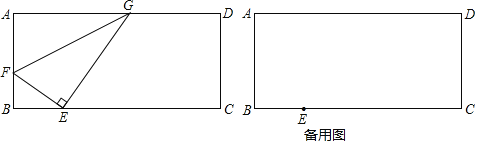
(1)当点F与点A重合时,点G恰好到达点D,此时x= ,当EF⊥BC时,x= ;
(2)求S关于x的函数解析式,并直接写出自变量x的取值范围;
(3)当S=15时,求此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4张卡片,卡片上分别标有数字1、-2、-3、4,它们除了标有的数字不同之外再也没有其它区别,小芳从盒子中随机抽取一张卡片.
(1)求小芳抽到负数的概率;
(2)若小明再从剩余的三张卡片中随机抽取一张,请你用树状图或列表法,求小明和小芳两人均抽到负数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C,D为![]() 上的点,且
上的点,且![]() =
=![]() ,延长AD,BC相交于点E,连接OD交AC于点F.
,延长AD,BC相交于点E,连接OD交AC于点F.
(1)求证:△ABC≌△AEC;
(2)若OA=3,BC=4,求AD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com