
【题目】如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD, 
(1)求抛物线的解析式;
(2)设点P(x,y)是第一象限内该抛物线上的一个动点,△PCD的面积为S,求S关于x的函数关系式,写出自变量x的取值范围,并求当x取多少时,S的值最大,最大是多少?
【答案】
(1)解:∵OC=4,OD=2,
∴DM=6,
∴点M(2,6),
设y=a(x﹣2)2+6,代入(0,4)得:a=﹣ ![]() ,
,
∴该抛物线解析式为y=﹣ ![]() (x﹣2)2+6
(x﹣2)2+6
(2)解:设点P(x,﹣ ![]() (x﹣2)2+6),即(x,﹣
(x﹣2)2+6),即(x,﹣ ![]() x2+2x+4),
x2+2x+4),
过点P作x轴的垂线,交直线CD于点F,
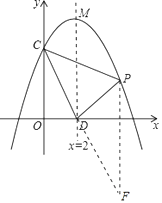
设直线CD为y=kx+4,代入(2,0)得k=﹣2,即y=﹣2x+4,
∴点F(x,﹣2x+4),
∴PF=﹣ ![]() x2+2x+4﹣(﹣2x+4)=﹣
x2+2x+4﹣(﹣2x+4)=﹣ ![]() x2+4x,
x2+4x,
∴S= ![]() 2(﹣
2(﹣ ![]() x2+4x)=﹣
x2+4x)=﹣ ![]() x2+4x,
x2+4x,
令y=a(x﹣2)2+6=0,
解得x1=2+2 ![]() ,x2=2﹣2
,x2=2﹣2 ![]() (舍去),
(舍去),
∴0<x<2+2 ![]() ,
,
∵S=﹣ ![]() x2+4x=﹣
x2+4x=﹣ ![]() (x﹣4)2+8,
(x﹣4)2+8,
∴当x=4时,S有最大值为8.
【解析】(1)由OC与OD的长,求出MD的长,确定出M坐标,设y=a(x﹣2)2+6,把C坐标代入求出a的值,即可确定出抛物线解析式;(2)由抛物线解析式设出P坐标,过点P做x轴的垂线,交直线CD于点F,利用待定系数法求出直线CD解析式,进而表示出F坐标,得到PF的表达式,表示出S与x的函数解析式,利用二次函数性质求出S最大值时x的值即可.
【考点精析】认真审题,首先需要了解二次函数的最值(如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a).


科目:初中数学 来源: 题型:
【题目】一个公共房门前的台阶高出地面2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( )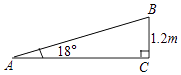
A.斜坡AB的坡度是18°
B.斜坡AB的坡度是tan18°
C.AC=2tan18°米
D.AB= ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
(1)参加朗诵比赛的学生共有人,并把条形统计图补充完整理;
(2)扇形统计图中,m= , n=;C等级对应扇形有圆心角为度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.求四边形AEBD的面积. 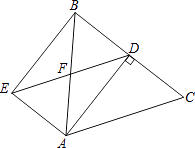
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个袋子中装有3个红球和2个黄球,这些球的形状、大小.质地完全相同,在看不到球的条件下,随机从袋子里同时摸出2个球,其中2个球的颜色相同的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是安装在斜屋面上的热水器,图2是安装该热水器的侧面示意图.已知,斜屋面的倾斜角为25°,长为2.1米的真空管AB与水平线AD的夹角为40°,安装热水器的铁架水平横管BC长0.2米,求 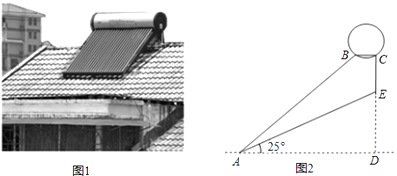
(1)真空管上端B到AD的距离(结果精确到0.01米);
(2)铁架垂直管CE的长(结果精确到0.01米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,点P在矩形ABCD内.若AB=4cm,BC=6cm,AE=CG=3cm,BF=DH=4cm,四边形AEPH的面积为5cm2 , 则四边形PFCG的面积为cm2 . 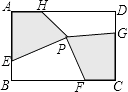
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com