
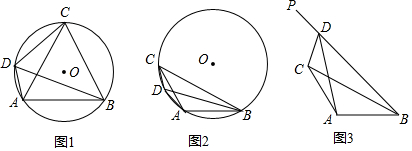
分析 (1)如图1,BD=CD+AD,在长边BD上截取BE=CD,再证明DE=AD即可,通过证明△ADC≌△AEB和△ADE是等边三角形可以得出结论;
(2)如图2,作辅助线,构建全等三角形和直角三角形,先证明∠CAB=∠DAE=120°,再证等腰△DAE得
∠ADE=30°,由30°的余弦可以得出DF与AD的关系,并由等腰三角形三线合一的性质得:DE=2DF,所以DE=$\sqrt{3}$AD,并利用线段的差代入得出结论:BD-CD=$\sqrt{3}$AD;
(3)如图3,作辅助线,构建全等三角形和直角三角形,与(2)类似可得出结论:BD+CD=$\sqrt{3}$AD;
解答  解:如图1,(1)BD=CD+AD,理由是:
解:如图1,(1)BD=CD+AD,理由是:
在BD上取一点E,使BE=CD,连接AE,
∵△ABC为正三角形,
∴∠ACB=60°,AC=AB,
∵∠ACD=∠ABD,
∴△ADC≌△AEB,
∴AD=AE,
∵∠ADB=∠ACB=60°,
∴△ADE是等边三角形,
∴DE=AD,
∴BD=DE+BE=AD+CD;
故答案为:BD=CD+AD;
(2)证明:如图2,过A作AF⊥BD于F,在BD上取一点E,使BE=CD,连接AE,
∵AC=AB,∠ACD=∠ABD,
∴△ACD≌△ABE,
∴AD=AE,∠DAC=∠EAB,
∴∠CAB=∠DAE,
∵∠CAB=120°,
∴∠DAE=120°,
在等腰△DAE中,∠ADE=$\frac{180°-120°}{2}$=30°,
∵AF⊥DE,
∴DF=EF,
cos30°=$\frac{DF}{AD}$,
∴DF=$\frac{\sqrt{3}}{2}$AD,
∴DE=$\sqrt{3}$AD,
∵DE=BD-BE=BD-CD,
∴BD-CD=$\sqrt{3}$AD;
(3)如图3,延长BD至E,使BE=CD,连接AE,过A作AF⊥BD于F,
∵∠BAC=120°,AB=AC,
∴∠ACB=∠ABC=30°,
∵∠CDP=120°,
∴∠CDP=∠DCB+∠DBC=120°,
∴∠DCB=120°-∠DBC,
∴∠DCA=∠DCB+∠ACB=120°-∠DBC+30°=150°-∠DBC,
∵∠ABE=180°-∠DBC-∠ABC=180°-30°-∠DBC=150°-∠DBC,
∴∠DCA=∠ABE,
∴△ADC≌△AEB,
∴AE=AD,∠CAD=∠BAE,
∴∠DAE=∠CAB=120°,
∴∠ADE=∠AED=30°,
同(2)得:点F是DE的中点,DF=$\frac{\sqrt{3}}{2}$AD,DE=$\sqrt{3}$AD,
∴DE=BD+BE=BD+CD=$\sqrt{3}$AD(0°<α<150°).
点评 本题是圆的综合题,其中涉及到圆周角定理、全等三角形、相似三角形、等腰三角形和等边三角形的性质和判定等知识,综合性较强,难度适中,恰当地作辅助线构建△AEB≌△ADC是解题的关键;在几何证明中,线段的和或差是一个难点,常用的思路为:①截,在长边上截取短边的长,②接,延长短边等于长边.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 8.01346 | B. | 8.0134×106 | C. | 8.0134×107 | D. | 8.0134×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=CD,AD=BC | B. | AB∥AD,CB∥CD | C. | AB∥CD,AD=BC | D. | ∠A=∠B,∠C=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
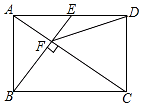 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列四个结论:
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列四个结论:| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com