
【题目】如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
实验与操作:
根据要求进行尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法)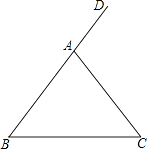
(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE,CF.
猜想并证明:
判断四边形AECF的形状并加以证明.
【答案】
(1)解:如图所示
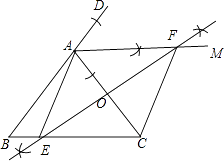
(2)解:四边形AECF的形状为菱形.理由如下:
∵AB=AC,
∴∠ABC=∠ACB,
∵AM平分∠DAC,
∴∠DAM=∠CAM,
而∠DAC=∠ABC+∠ACB,
∴∠CAM=∠ACB,
∴EF垂直平分AC,
∴OA=OC,∠AOF=∠COE,
在△AOF和△COE中
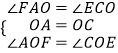 ,
,
∴△AOF≌△COE,
∴OF=OE,
即AC和EF互相垂直平分,
∴四边形AECF的形状为菱形
【解析】先作以个角的交平分线,再作线段的垂直平分线得到几何图形,由AB=AC得∠ABC=∠ACB,由AM平分∠DAC得∠DAM=∠CAM,则利用三角形外角性质可得∠CAM=∠ACB,再根据线段垂直平分线的性质得OA=OC,∠AOF=∠COE,于是可证明△AOF≌△COE,所以OF=OE,然后根据菱形的判定方法易得四边形AECF的形状为菱形.
【考点精析】通过灵活运用角平分线的性质定理和线段垂直平分线的性质,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,以B为圆心,BC长为半径画弧,分别交AC、AB于D,E两点,并连接BD,DE.若∠A=30°,AB=AC,则∠BDE的度数为何( )
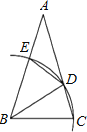
A.45 B.52.5 C.67.5 D.75
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:设a→,=(x1,y1),b→,=(x2,y2),如果a→,∥b→,,则x1·y2=x2·y1.根据该材料填空:已知a→,=(4,3),b→,=(8,m),且a→,∥b→,,则m=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),B(0,1)是正方形OBB1C的两个顶点,以它的对角线OB1为一边作正方形OB1B2C1 , 以正方形OB1B2C1的对角线OB2为一边作正方形OB2B3C2 , 再以正方形OB2B3C2的对角线OB3为一边作正方形OB3B4C3 , …,依次进行下去,则点B6的坐标是 . 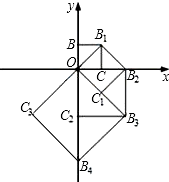
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,∠A=∠F,试说明∠C=∠D.
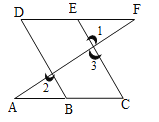
解:∵ ![]() ( 已知 )
( 已知 )
![]() ( )
( )
∴![]() ( 等量代换 )
( 等量代换 )
∴![]() ( )
( )
∴![]() ( 两直线平行,同位角相等 )
( 两直线平行,同位角相等 )
∵ ![]() ( 已知 )
( 已知 )
∴![]() ( )
( )
∴![]() ( 两直线平行,内错角相等 )
( 两直线平行,内错角相等 )
∴![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
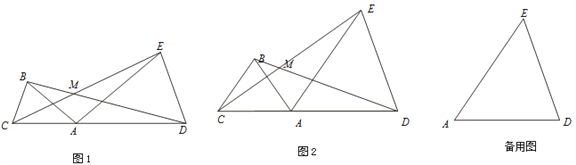
【题目】已知:点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段 BD、CE交于点M.
(1)如图1,若AB=AC,AD=AE
①问线段BD与CE有怎样的数量关系?并说明理由;②求∠BMC的大小(用α表示);
(2)如图2,若AB= BC=kAC,AD =ED=kAE 则线段BD与CE的数量关系为 ,∠BMC= (用α表示);
(3)在(2)的条件下,把△ABC绕点A逆时针旋转180°,在备用图中作出旋转后的图形(要求:尺规作图,不写作法,保留作图痕迹),连接 EC并延长交BD于点M.则∠BMC= (用α表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com