
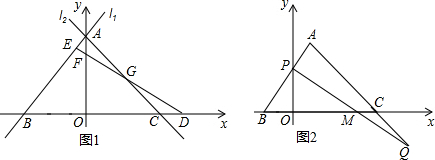
���� ��1���������ֱ��$y=\frac{4}{3}x+4$��y��Ľ���A�����꣬���ɵõ���OA�ij��ȣ��ɵ�D������ɵ�OD�ij��ȣ��ɵ�OA=OD������DE��AB��E���ɵá�AEF=90�㣬���ԡ�AFE+��EAF=90�㣬����Ϊ��OFD+��FDO=90�㣬����Ϊ��AFE=��OFD���ɵá�EAF=��FDO������Ϊ��AOB=��DOF=90�㣬�Ӷ����ж���ABO�ա�DFO��������õ�B�����꣬���ɢٿ�֪��ABO�ա�DFO���ɵ�OF=OB���Ӷ�����õ�F�����꣬�����ô���ϵ���������ֱ��DF�Ľ���ʽ�������ֱ��AC�Ľ���ʽ������������ʽ����Ϊ�����飬������ɵõ���G�����ꣻ
��2������P��PN��AB��BC�ڵ�N������ƽ���ߵ����ʿɵá�MPN=��Q��Ȼ��֤��PN=BQ�������á��ǽDZߡ�֤����QCM�͡�PNMȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�MN=BM���ٸ��ݵ������������ߺ�һ�����ʿɵ�ON=OC���Ӷ�֤��OM=$\frac{1}{2}$BC���Ƕ�ֵ����3������P��PN��AC��BC�ڵ�N������ƽ���ߵ����ʿɵá�MPN=��Q��Ȼ��֤��PN=CQ�������á��ǽDZߡ�֤����QCM�͡�PNMȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�MN=CM���ٸ��ݵ������������ߺ�һ�����ʿɵ�ON=OB���Ӷ�֤��OM=$\frac{1}{2}$BC���Ƕ�ֵ��
��3��ȡAC���е�T���Ե�TΪԲ�ģ�ACΪ�뾶��Բ������OT����Բ�ڵ�H�����ʱOH��ֵ��С������A��T�ֱ���x��Ĵ��ߣ�����ֱ�ΪI��S���ɣ�1����2����֪������ABCΪ���������Σ����ɵ�A��B��C����������AC��BC��AI�ij��ȣ������������ε���λ�ߵ����ʼ������TS��IS�ij��ȣ����ɵõ���T�����꣬�����ù��ɶ�����������߶�OT�ij��ȣ��Ӷ��õ��߶�OH����Сֵ��
��� �⣺��1����ͼ1����֤��������ֱ��$y=\frac{4}{3}x+4$����x=0����y=4��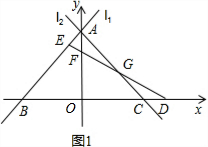
���A����������0��4����
��OA=4��
��D���������4��0����
��OD=4��
��OA=OD��
��DE��AB��E��
���AEF=90�㣬
���AFE+��EAF=90�㣬
�ߡ�OFD+��FDO=90�㣬��AFE=��OFD��
���EAF=��FDO������Ϊ��AOB=��DOF=90�㣬
�ڡ�ABO���DOF�У�
$\left\{\begin{array}{l}{��BAO=��FDO}\\{OA=OD}\\{��AOB=��DOF}\end{array}\right.$
���ABO�ա�DFO��
�ڶ���ֱ��$y=\frac{4}{3}x+4$����y=0����x=-3��
���B��������-3��0����
�ߡ�ABO�ա�DFO��
��OF=OB=3��
���F��������0��3����
��ֱ��DF�Ľ���ʽΪy1=k1x+b1��
�ѵ�F��0��3������D��4��0������ã�
$\left\{\begin{array}{l}{{b}_{1}=3}\\{{4k}_{1}{+b}_{1}=0}\end{array}\right.$
���$\left\{\begin{array}{l}{{k}_{1}=-\frac{3}{4}}\\{{b}_{1}=3}\end{array}\right.$
��ֱ��DF�Ľ���ʽΪy=-$\frac{3}{4}$x+3��
��ֱ��AC�Ľ���ʽΪy2=k2x+b2��
�ѵ�A��0��4������C�����꣨3��0������ã�
$\left\{\begin{array}{l}{{b}_{2}=4}\\{{3k}_{2}{+b}_{2}=0}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{{k}_{2}=-\frac{4}{3}}\\{{b}_{2}=4}\end{array}\right.$
��ֱ��AC�Ľ���ʽΪy=-$\frac{4}{3}$x+4��
��$\left\{\begin{array}{l}{y=-\frac{3}{4}x+3}\\{y=-\frac{4}{3}x+4}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{x=\frac{12}{7}}\\{y=\frac{12}{7}}\end{array}\right.$
���G��������$\frac{12}{7}$��$\frac{12}{7}$����
��2��OM�ij��Ȳ��ᷢ���仯����ͼ2����P����PN��AC��BC��N�㣬
���MPN=��Q����ACB=��PNB��
�ɣ�1����ͼ1�ɵ�OB=OC=3��BC=6��
��AB=AC��
���ACB=��ABC��
���PNB=��PBC��
��PN=PB��
��BP=CQ��
��PN=CQ��
�ߡ�PMN=��QMC��
�ڡ�QCM���PNM�У�
$\left\{\begin{array}{l}{��PMN=��QMC}\\{��MPN=��MQC}\\{PN=QC}\end{array}\right.$
���QCM�ա�PNM��AAS����
��MN=CM��
��PB=PN��PO��BN��
��ON=OB��
��CM+MN+ON+OB=BC��
��OM=MN+ON=$\frac{1}{2}$BC=3��
���Ƕ�ֵ��
��3����ͼ3��ȡAC���е�T���Ե�TΪԲ�ģ�ACΪ�뾶��Բ������OT����Բ�ڵ�H������A��T�ֱ���x��Ĵ��ߣ�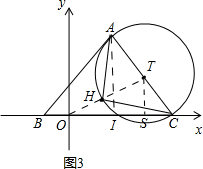
�ɣ�1����2����֪��ABC�ǵ��������Σ�
AC=5��BC=6��AI=4��
��AI��x�ᣬTS��x�ᣬ
��AI��TS��
�ߵ�T��AC���е㣬
��TS�ǡ�AIC����λ�ߣ�
��TS=2��IS=1.5��
��OS=1.5+a��
���T��������1.5+a��2����
��Rt��OTS��
OT=$\sqrt{{2}^{2}{+��1.5+a��}^{2}}$��
��OH=OT-TH=$\sqrt{{2}^{2}{+��1.5+a��}^{2}}$-2.5��
���� �����ۺϿ�����һ�κ���������ϵ������ֱ�߽���ʽ����ֱ�ߵĽ������⣬ȫ�������ε��ж������ʣ��ۺ��Խ�ǿ����ϵ�Ƚϸ��ӣ����ѶȲ���ֻҪ��ϸ������������⣬�㲻�ѽ��


 ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д� С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2+4b2 | B�� | a2+2ab+2b2 | C�� | a2+4ab+2b2 | D�� | a2+4ab+4b2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڡ�ABC�У�D��E�ֱ��DZ�AB��AC���е㣬BC=4����������в���ȷ���ǣ�������
��ͼ���ڡ�ABC�У�D��E�ֱ��DZ�AB��AC���е㣬BC=4����������в���ȷ���ǣ�������| A�� | DE=2 | |
| B�� | ��ADE��������ABC�����֮��Ϊ1��4 | |
| C�� | ��ADE�ס�ABC | |
| D�� | ��DEC���ܳ����ABC���ܳ�֮��Ϊ1��2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com