
分析 (1)由关于x的一元二次方程x2-x+$\frac{1}{4}$m=0有实数根,根据判别式得到关于m的不等式,然后解不等式即可求出m的取值范围;
(2)根据(1)的结果和m为正整数可求特殊的m值,然后方程的解就可以求出.
解答 解:(1)∵关于x的一元二次方程x2-x+$\frac{1}{4}$m=0有实数根,
∴△=b2-4ac≥0,
即(-1)2-4×1×$\frac{1}{4}$m≥0,
解这个不等式得m≤1,
∴m≤1;
(2)∵m≤1且m为正整数,
∴m=1.
当m=1时,此方程为x2-x+$\frac{1}{4}$=0,
∴此方程的根为x1=x2=$\frac{1}{2}$.
点评 本题考查了一元二次方程根的判别式(△=b2-4ac),一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
也考查了一元二次方程的解法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
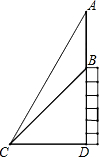 如图,楼顶有一根天线AB,为了测量天线的高度,在地面点C处测得楼顶B点的仰角∠BCD为45°,测得天线顶点A的仰角∠ACD为60°,且点C到楼的距离CD为15米,求天线AB的长(结果保留根号).
如图,楼顶有一根天线AB,为了测量天线的高度,在地面点C处测得楼顶B点的仰角∠BCD为45°,测得天线顶点A的仰角∠ACD为60°,且点C到楼的距离CD为15米,求天线AB的长(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com