
【题目】重庆一中各校区的中考体育学科考试在四月中旬圆满结束,在长期备战体考的过程中,学生的身体素质也在悄然发生变化.某体能测试机构将我校初三学生在体育测试中的成绩转换成弹跳力和臂力两项指标(百分制)作为体能测试成绩,并根据数据分析研究如何进一步提高学生的身体素质.
数据收集该机构计划选取100名学生的体能测试成绩作为样本,提供了以下三种抽样调查方法:
A.抽取初三年级皇冠校区的100名学生的体能测试成绩组成样本
B.抽取全年级体育成绩较好的学生共100名学生的体能测试成绩组成样本
C.从全年级中随机选取男、女各50名学生的体能测试成绩组成样本
数据整理与描述
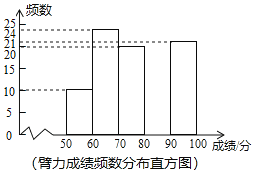
a.数据分成5组:90≤x≤100,80≤x<90,70≤x<80,60≤x<70,50≤x<60,其中90分以上为优秀.弹跳力成绩统计表和臂力成绩频数分布直方图如下:
弹跳力成绩 | 划记 | 人数 |
90≤x≤100 | p | |
80≤x<90 | 正正正正正正丅 | 37 |
70≤x<80 | 正正正正正 | 23 |
60≤x<70 | 正一 | 6 |
50≤x<60 | 正 | 5 |
合计 | 100 | 100 |
(弹跳力成绩统计表)
b.臂力成绩在70≤x<80这一组的具体分数如下:
70 71 71 71.5 72 73 73.5 74 74 74
74.5 74.5 75 75.5 75.5 76 76 77 78 79
c.弹跳力和臂力两项指标成绩的平均数、中位数、众数、优秀率统计如下:
体能指标 | 平均数(分) | 中位数(分) | 众数(分) | 优秀率 |
弹跳力 | 82.5 | 89 | 83 | m |
臂力 | 77 | n | 81 | 21% |
数据分析根据以上信息,回答下列问题:
(1)上述三种抽样方法中,你认为最合理的是 (填字母);
(2)补全臂力成绩频数分布直方图,并整理数据得,m= ,n= ;
(3)在此次测试中,某学生的弹跳力成绩为87分,臂力成绩为78分,这名学生成绩排名更靠前的指标是 (填“弹跳力”或“臂力”),理由是 .
【答案】(1)C;(2)补全直方图见解析;29%,76;(3)臂力,弹跳力成绩为87分,小于其中位数89分,臂力成绩为78分,大于其中位数76分.
【解析】
(1)根据抽样调查的数据需要具有代表性求解可得;
(2)总人数减去臂力成绩的其它分组的成绩可得80≤x<90的频数,从而补全图形;总人数减去弹跳力成绩的其它分组的成绩可得90≤x<100的频数p的值,继而可得m的值,根据中位数的概念可得n的值;
(3)从中位数的意义解答即可得.
(1)上述三种抽样方法中,你认为最合理的是C.从全年级中随机选取男、女各50名学生的体能测试成绩组成样本,
故选:C.
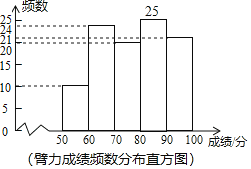
(2)臂力成绩频数分布直方图中,80≤x<90的频数为100﹣(10+24+20+21)=25,
补全直方图如下:
∵p=100﹣(37+23+6+5)=29,
∴m=![]() ×100%=29%;
×100%=29%;
n=![]() =76,
=76,
故答案为:29%,76;
(3)∵弹跳力成绩为87分,小于其中位数89分,臂力成绩为78分,大于其中位数76分,
∴弹跳力成绩在50名之后,臂力成绩在50名之前,
∴这名学生成绩排名更靠前的指标是臂力成绩,
故答案为:臂力;弹跳力成绩为87分,小于其中位数89分,臂力成绩为78分,大于其中位数76分.


科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
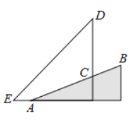
【题目】在屋楼崮西侧一个坡度(或坡比)![]() 的山坡
的山坡![]() 上发现有一棵古树
上发现有一棵古树![]() .测得古树底端
.测得古树底端![]() 到山脚点
到山脚点![]() 的距离
的距离![]() 米,在距山脚点
米,在距山脚点![]() 水平距离
水平距离![]() 米的点
米的点![]() 处,测得古树顶端
处,测得古树顶端![]() 的仰角
的仰角![]() (古树
(古树![]() 与山坡
与山坡![]() 的剖面、点
的剖面、点![]() 在同一平面上,古树
在同一平面上,古树![]() 与直线
与直线![]() 垂直),则古树
垂直),则古树![]() 的高度约为
的高度约为![]() ( )
( )
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A坐标为(-8,0),点B坐标为(0,6),⊙O的半径为4(O为坐标原点),点C是⊙O上一动点,过点B作直线AC的垂线BP,P为垂足.点C在⊙O上运动一周,则点P运动的路径长等于________.

查看答案和解析>>
科目:初中数学 来源: 题型:
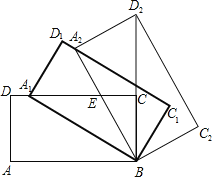
【题目】如图,矩形ABCD中,AB=m,BC=n,将此矩形绕点B顺时针方向旋转θ(0°<θ<90°)得到矩形A1BC1D1,点A1在边CD上.
(1)若m=2,n=1,求在旋转过程中,点D到点D1所经过路径的长度;
(2)将矩形A1BC1D1继续绕点B顺时针方向旋转得到矩形A2BC2D2,点D2在BC的延长线上,设边A2B与CD交于点E,若![]() =
=![]() ﹣1,求
﹣1,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+
x2+![]() x﹣4与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
x﹣4与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
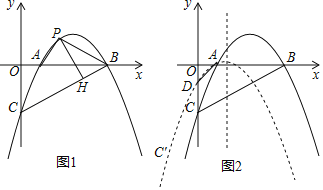
(1)连接BC,P是线段BC上方抛物线上的一动点,过点P作PH⊥BC于点H,当PH长度最大时,在△APB内部有一点M,连接AM、BM、PM,求AM+![]() BM+PM的最小值.
BM+PM的最小值.
(2)若点D是OC的中点,将抛物线y=![]() x2+
x2+![]() x﹣4沿射线AD方向平移
x﹣4沿射线AD方向平移![]() 个单位得到新抛物线y′,C′是抛物线y′上与C对应的点,抛物线y'的对称轴上有一动点N,在平面直角坐标系中是否存在一点S,使得C′、N、B、S为顶点的四边形是矩形?若存在,请直接写出点S的坐标;若不存在,请说明理由.
个单位得到新抛物线y′,C′是抛物线y′上与C对应的点,抛物线y'的对称轴上有一动点N,在平面直角坐标系中是否存在一点S,使得C′、N、B、S为顶点的四边形是矩形?若存在,请直接写出点S的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
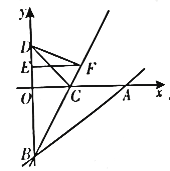
【题目】如图,在平面直角坐标系xOy中,直线![]() 交x轴正半轴于点A,交y轴负半轴于点B,点C在线段OA上,将
交x轴正半轴于点A,交y轴负半轴于点B,点C在线段OA上,将![]() 沿直线BC翻折,点A与y轴上的点D(0,4)恰好重合.
沿直线BC翻折,点A与y轴上的点D(0,4)恰好重合.
(1)求直线AB的表达式.
(2)已知点E(0,3),点P是直线BC上的一个动点(点P不与点B重合),连接PD,PE,当![]() PDE的周长取得最小值时,求点P的坐标。
PDE的周长取得最小值时,求点P的坐标。
(3)在坐标轴上是否存在一点H,使得![]() HAB和
HAB和![]() ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由。
ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于C、D两点,与x轴交于点A.
交于C、D两点,与x轴交于点A.
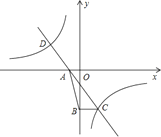
(1)求n的取值范围和点A的坐标;
(2)过点C作CB⊥y轴,垂足为B,若S△ABC=4,求双曲线的解析式;
(3)在(1)、(2)的条件下,若AB=![]() ,求点C和点D的坐标并根据图象直接写出反比例函数的值小于一次函数的值时,自变量x的取值范围.
,求点C和点D的坐标并根据图象直接写出反比例函数的值小于一次函数的值时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
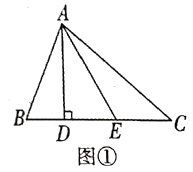
(1)如图①在![]() 中,
中,![]() 是
是![]() 边
边![]() 的高,点
的高,点![]() 是
是![]() 上任意一点,若
上任意一点,若![]() 则
则![]() 的最小值为_ ;
的最小值为_ ;
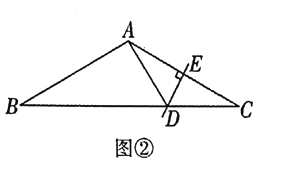
(2)如图②,在等腰![]() 中,
中,![]() 是
是![]() 的垂直平分线,分别交
的垂直平分线,分别交![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的周长;
的周长;
问题解决:
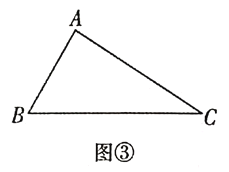
(3)如图③,某公园管理员拟在园内规划一个![]() 区域种植花卉,且为方便游客游览,欲在各顶点之间规划道路
区域种植花卉,且为方便游客游览,欲在各顶点之间规划道路![]() 和
和![]() ,满足
,满足![]() 点
点![]() 到
到![]() 的距离为
的距离为![]() .为了节约成本,要使得
.为了节约成本,要使得![]() 之和最短,试求
之和最短,试求![]() 的最小值(路宽忽略不计).
的最小值(路宽忽略不计).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com