
【题目】如图,在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=-x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点B的坐标为(-1,0)
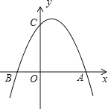
(1)求抛物线的解析式;
(2)点D的坐标为(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,求点P的坐标.
【答案】(1)y=﹣x2+2x+3;(2)点P的坐标为(1+![]() ,2)或(1﹣
,2)或(1﹣![]() ,2).
,2).
【解析】
(1)求出A、B坐标,利用待定点C的坐标为(0,3),点D(1,0),
(2)由点C的坐标为(0,3),点D(1,0),可知满足条件的点P的纵坐标为2,解方程-x2+2x+3=2即可得到点P的横坐标,由此即可解决问题.
解:(1)∵抛物线的对称轴为直线x=1,y=﹣x2+bx+c与x轴交于点A和点B,
∴由题意可求点A的坐标为(3,0).
将点A(3,0)和点B(﹣1,0)代入y=﹣x2+bx+c,
得 ![]() ,
,
解得 ![]() ,
,
∴抛物线的解析式y=﹣x2+2x+3.
(2)如图,
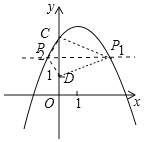
∵点C的坐标为(0,3),点D(1,0),
∴满足条件的点P的纵坐标为2.
∴﹣x2+2x+3=2.
解得 x1=1+![]() ,x2=1﹣
,x2=1﹣![]() ,
,
∴点P的坐标为(1+![]() ,2)或(1﹣
,2)或(1﹣![]() ,2).
,2).


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
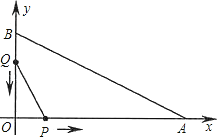
【题目】如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,过点A作直线EF.
(1)如图①,AB是直径,要使EF是⊙O的切线,还须添加一个条件是(只需写出三种情况).
(ī) (īī) (īīī)
(2)如图(2),若AB为非直径的弦,∠CAE=∠B,则EF是⊙O的切线吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2x+3与x轴交于A,B两点,点A在点B的左侧.
(1)求A,B两点的坐标和此抛物线的对称轴;
(2)设此抛物线的顶点为C,点D与点C关于x轴对称,求四边形ACBD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若存在过点P的直线l交⊙C于异于点P的A,B两点,在P,A,B三点中,位于中间的点恰为以另外两点为端点的线段的中点时,则称点P为⊙C 的相邻点,直线l为⊙C关于点P的相邻线.
(1)当⊙O的半径为1时,
①分别判断在点D(![]() ,
, ![]() ),E(0,﹣
),E(0,﹣![]() ),F(4,0)中,是⊙O的相邻点有 ;
),F(4,0)中,是⊙O的相邻点有 ;
②请从①中的答案中,任选一个相邻点,在图1中做出⊙O关于它的一条相邻线,并说明你的作图过程;
③点P与点O的距离d满足范围___________________时,点P是⊙O的相邻点;
④点P在直线y=﹣x+3上,若点P为⊙O的相邻点,求点P横坐标x的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣![]() x+2
x+2![]() 与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标x的取值范围.
与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),如果点Q(x,y′)的纵坐标满足y′=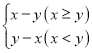 ,那么称点Q为点P的“关联点”.
,那么称点Q为点P的“关联点”.
(1)请直接写出点(3,5)的“关联点”的坐标 ;
(2)如果点P在函数y=x﹣2的图象上,其“关联点”Q与点P重合,求点P的坐标;
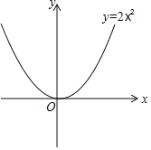
(3)如果点M(m,n)的“关联点”N在函数y=2x2的图象上,当0≤m≤2时,求线段MN的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究函数![]() 的图象与性质.
的图象与性质.
小娜根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小娜的探究过程,请补充完整:
的图象与性质进行了探究.下面是小娜的探究过程,请补充完整:
(1)下表是x与y的几组对应值.
x | … |
|
| 0 |
| 2 |
| 3 | … |
y | … |
|
| 0 | m | n |
| 3 | … |
请直接写出:m= ,n= ;
(2)如图,小娜在平面直角坐标系xOy中,描出了上表中已经给出的各组对应值为坐标的点,请再描出剩下的两个点,并画出该函数的图象;

(3)结合画出的函数图象,解决问题:若方程![]() 有三个不同的解,记为x1, x2, x3,且x1< x2<x3. 请直接写出x1+ x2+x3的取值范围.
有三个不同的解,记为x1, x2, x3,且x1< x2<x3. 请直接写出x1+ x2+x3的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y=![]() 的图象与性质.小美根据学习函数的经验,对函数y=
的图象与性质.小美根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究下面是小美的探究过程,请补充完整:
的图象与性质进行了探究下面是小美的探究过程,请补充完整:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | -2 | - | -1 | - |
|
| 1 | 2 | 3 | 4 | … |
y | 0 | - | -1 | - |
|
|
| m |
|
| … |
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
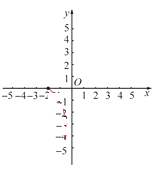
(4)结合函数的图象,写出该函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民的交通消费可分为交通工具、交通工具使用燃料、交通工具维修、市内公共交通、城市间交通五项.该市统计局根据当年各项的权重及各项价格的涨幅,计算当年居民交通消费价格的平均涨幅.2017年该市的有关数据如下表所示.
交通工具 | 交通工具使用燃料 | 交通工具维修 | 市内公共交通 | 城市间交通 | |
占交通消费的比例 | 22% | 13% | 5% | P | 26% |
相对上一年价格的涨幅 | 1.5% | m% | 2% | 0.5% | 1% |
(1)求p的值;
(2)若2017年该市的居民交通消费相对上一年价格的平均涨幅为1.25%,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com