
已知:如图,∠B=90°,AB∥DF,AB=3cm,BD=8cm,点C是线段BD上一动点,点E是直线DF上一动点,且始终保持AC⊥CE.

(1)试说明:∠ACB =∠CED
(2)若AC=CE ,试求DE的长
(3)在线段BD的延长线上,是否存在点C,使得AC=CE,若存在,请求出DE的长及△AEC的面积;若不存在,请说明理由。
(1)说明见解析; (2)5cm;(3)65cm2.
【解析】
试题分析:(1)根据平行线的性质和三角形的内角和定理求出即可;
(2)根据全等得出对应边相等,即可得出答案;
(3)求出两三角形全等,得出对应边相等,再根据勾股定理和三角形面积公式求出即可.
试题解析:(1)∵∠B=90°,AB∥DF,
∴∠D=∠B=90°,
∵AC⊥CE,
∴∠ACE=90°,
∴∠ECD+∠CED=90°,∠ACB+∠ECD=90°,
∴∠ACB=∠CED;
(2)∵在△ABC和△CDE中

∴△ABC≌△CDE(AAS),
∴AB=CD=3cm,
∴DE=BC=8cm-3cm=5cm;
(3)∵∠B=90°AB∥DF,
∴∠CDE=∠B=90°,
∵AC⊥CE,
∴∠ACE=90°,
∴∠ECD+∠ACB=90°,∠ACB+∠BAC=90°,
∴∠ECD=∠BAC;
当CD=AB=3cm时,AC=CE,
∵在△ABC和△CDE中

∴△ABC≌△CDE(ASA),
∴AC=CE,DE=BD=8cm,
∵AB=3cm,BC=BD+CD=8cm+3cm=11cm,
∴在Rt△ABC中,由勾股定理得;AC=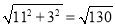
∵∠ACE=90°,
∴△AEC的面积是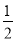 ×AC×CE=
×AC×CE=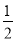 ×
×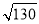 ×
×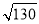 =65cm2.
=65cm2.
考点:全等三角形的判定与性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年江苏省无锡市新区八年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题6分)如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=2,求∠DFE的度数与EC的长.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市新区九年级上学期期中考试数学试卷(解析版) 题型:选择题
三角形两边的长是3和4,第三边的长是方程 的根,则该三角形的周长为 ( )
的根,则该三角形的周长为 ( )
A.12 B.14 C.12或14 D.以上都不对
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市新区七年级上学期期中考试数学试卷(解析版) 题型:选择题
下列比较大小正确的是 ( )
A.
B.-(-21)<+(-21)
C.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市惠山区八年级上学期期中考试数学试卷(解析版) 题型:解答题
尺规作图:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵桂花树.如图,要求桂花树的位置(视为点P),到花坛的两边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种桂花树的位置点P(不写作法,保留作图痕迹).

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市惠山区九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分8分)如图,有一长方形的仓库,一边长为5米.现要将它改建为简易住房,改建
后的住房分为客厅、卧室和卫生间三部分,其中客厅和卧室都为正方形,且卧室的面积大于卫生间的面积.若改建后卫生间的面积为6平方米,试求长方形仓库另一边的长.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市惠山区七年级上学期期中考试数学试卷(解析版) 题型:选择题
在一条笔直的公路边,有一些树和路灯,每相邻的两盏灯之间有3棵树,相邻的树与树、树与灯间的距离是10m,如图,第一棵树左边5m处有一个路牌,则从此路牌起向右340m~380m之间树与灯的排列顺序是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com