
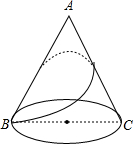
 有一圆锥形粮堆如图所示,其母线长为12m,底面直径长为6m,一只小猫从B处绕粮堆巡视一圈后又回到B处,则它所行走最短路程是
有一圆锥形粮堆如图所示,其母线长为12m,底面直径长为6m,一只小猫从B处绕粮堆巡视一圈后又回到B处,则它所行走最短路程是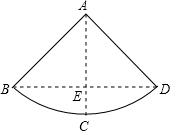 解:∵一圆锥形粮堆,其母线长为12m,底面直径长为6m,
解:∵一圆锥形粮堆,其母线长为12m,底面直径长为6m,| nπ×12 |
| 180 |
| π |
| 15 |
| π |
| 15 |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
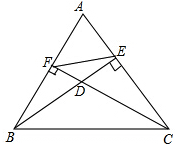 如图,BE、CF分别是△ABC的边AC、AB上的高,BE与CF相交于点D,求证:
如图,BE、CF分别是△ABC的边AC、AB上的高,BE与CF相交于点D,求证:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
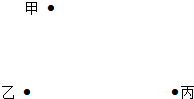 作图题:如图,现在甲、乙、丙三家公司共建一个污水处理站P,使得该站到乙、丙两家公司的距离相等,且使甲公司到污水处理站P的距离最短,试在图中确定污水处理站P的位置.(要求尺规作图,保留作图痕迹,不写作法,但要写结论)
作图题:如图,现在甲、乙、丙三家公司共建一个污水处理站P,使得该站到乙、丙两家公司的距离相等,且使甲公司到污水处理站P的距离最短,试在图中确定污水处理站P的位置.(要求尺规作图,保留作图痕迹,不写作法,但要写结论)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在矩形ABCD中,E是AD边上的一点,CE交对角线于点O,△DOE面积为2,△COD面积为8,
如图,在矩形ABCD中,E是AD边上的一点,CE交对角线于点O,△DOE面积为2,△COD面积为8,| DO |
| BO |
| DE |
| CD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com