如图.已知DE∥BC.AD:BD=2:3.则S△ADES△ABC= ．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

如图，已知DE∥BC，AD：BD=2：3，则

S△ADE

S△ABC

．

考点：相似三角形的判定与性质

专题：

分析：由条件可以求出AD：AB=2；5，再由条件可以得出△ADE∽△ABC，最后由相似三角形的性质就可以得出结论．

解答：解：∵AD：BD=2：3，
∴AD：AB=2：5，
∵在△ABC中，DE∥BC，
∴△ADE∽△ABC，
∴

S△ADE

S△ABC

=（

）²=

，
故答案为：

．

点评：本题考查了相似三角形的判定与性质．解题的关键是掌握相似三角形的面积比等于相似比的平方．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

已知一直角三角形纸片OAB，∠AOB=90°，OA=2，OB=4．将该纸片放在平面直角坐标系中（如图①），折叠该纸片，折痕与边OB交于点C，与边AB交于点D．
（1）若折叠后使点B与O重合（如图②），求点C的坐标及C、A两点的距离；
（2）若折叠后使点B与A重合（如图③），求点C的坐标；
（3）若折叠后点B落在边OA上的点为B′（如图④），设OB′=x，OC=y，求出y关于x的函数关系式，并写出定义域．

查看答案和解析>>

科目：初中数学 来源： 题型：

下列事件为不可能事件的是（　　）

A、某射击运动员射击一次，命中靶心

B、掷一次骰子，向上一面是3点

C、找到一个三角形，其内角和是200°

D、经过城市中某一有交通信号灯的路口遇到绿灯

查看答案和解析>>

科目：初中数学 来源： 题型：

已知a＜0，化简二次根式

-a3b

的结果是

．

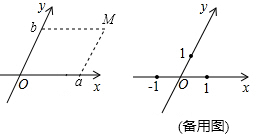
查看答案和解析>>

科目：初中数学 来源： 题型：

如图，类似于平面直角坐标系，我们现定义平面斜坐标系，∠xOy=60°，对于平面内任意一点M，过M点作两条直线分别平行于x轴和y轴，与x轴、y轴相交的点所表示的数为a和b，则M点的斜坐标为（a，b）．
（1）若A点的斜坐标为（-2，2），试在该坐标系中作出点A，并求点A到点O的距离；
（2）在斜坐标系xOy中，已知点B（4，0），点C（0，3），P（x，y）是线段BC上的任意一点，试说明3x+4y是一个定值；
（3）若问题（2）中的点P在直线BC上，其他条件都不变，试判断上述x，y之间的数量关系是否仍然成立；
（4）请在备用图上画出与方程2x-3y=6相对应的直线．