
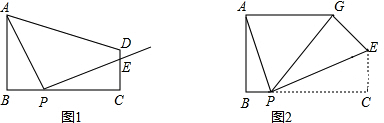
���� ��1���������������ε��ж������ʣ��ֱ�ó���$\frac{AB}{CE}$=$\frac{BP}{CP}$��$\frac{AB}{PC}$=$\frac{BP}{EC}$ʱ�������⣬����𰸼��ɣ�
��2��֤����ABP�ס�PCE�����ñ����߶ι�ϵ���y��x�ĺ�����ϵʽ�����ö��κ������ʣ���������ֵ���в���ʽȷ��m��ȡֵ��Χ��
��3�����ݷ��۵����ʼ���֪����������ֱ�������Σ����ù��ɶ������BP�ij��ȣ�
��� �⣺��1����BP=x��
��AB��BD��CD��BD��
���B=��D=90�㣬
�൱$\frac{AB}{CE}$=$\frac{BP}{CP}$��$\frac{AB}{PC}$=$\frac{BP}{EC}$ʱ��ʹ��P��A��B����Ϊ���������������P��C��E����Ϊ��������������ƣ�
���$\frac{18}{8}$=$\frac{x}{30-x}$���$\frac{18}{30-x}$=$\frac{x}{8}$��
��ã�x=$\frac{270}{13}$��x1=6��x2=24��
��BP�ij�����$\frac{270}{13}$��6��24��
��2���ߡ�APB+��CPE=90�㣬��CEP+��CPE=90�㣬
���APB=��CEP���֡ߡ�B=��C=90�㣬
���ABP�ס�PCE��
��$\frac{AB}{PC}$=$\frac{BP}{EC}$����$\frac{18}{m-x}$=$\frac{x}{y}$��
��y=-$\frac{1}{18}$x2+$\frac{m}{18}$x
=-$\frac{1}{18}$��x-$\frac{m}{2}$��2+$\frac{{m}^{2}}{72}$��
�൱x=$\frac{m}{2}$ʱ��yȡ�����ֵ�����ֵΪ$\frac{{m}^{2}}{72}$��
�ߵ�P���߶�BC���˶�ʱ����E�����߶�CD�ϣ�
��$\frac{{m}^{2}}{72}$��9��
���m��18$\sqrt{2}$��
��m��ȡֵ��ΧΪ��0��m��18$\sqrt{2}$��
�ʴ�Ϊ��0��m��18$\sqrt{2}$��
��3�����۵���֪��PG=PC��EG=EC����GPE=��CPE��
�֡ߡ�GPE+��APG=90�㣬��CPE+��APB=90�㣬
���APG=��APB��
�ߡ�BAG=90�㣬
��AG��BC��
���GAP=��APB��
���GAP=��APG��
��AG=PG=PC��
��ͼ2��ʾ���ֱ��ӳ�CE��AG�����ڵ�H��
����֪ABCHΪ���Σ�HE=CH-CE=18-y��GH=AH-AG=36-��36-x��=x��
��Rt��GHE�У��ɹ��ɶ����ã�GH2+HE2=GE2��
����x2+��18-y��2=y2������ã�x2-36y+324=0 ��
�ɣ�1����֪��y=-$\frac{1}{18}$x2+$\frac{m}{18}$x������m=36��
��y=-$\frac{1}{18}$x2+2x��
�����ʽ�����ã�3x2-8x+4=0��
��ã�x=18��x=6��
��BP�ij�Ϊ18��6��
���� ���⿼���˴��������ۺ��⡢���������Ρ����ɶ��������Ρ����Ρ��۵���������ϵʽ�����κ�����ֵ��֪ʶ�㣬���漰�����ڶ࣬��һ�����Ѷȣ�ע��ڣ�2��������mȡֵ��Χʱ���κ������ʵ�Ӧ�ã��Լ��ڣ�3�����й���ֱ�������εķ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
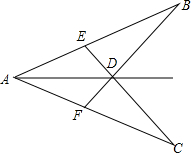 ��ͼ��AB=AC��D�ǡ�BAC�Ľ�ƽ�����ϵ�һ�㣬����CD���ӳ���AB��E������BD���ӳ���AC��F����֤��AE=AF��
��ͼ��AB=AC��D�ǡ�BAC�Ľ�ƽ�����ϵ�һ�㣬����CD���ӳ���AB��E������BD���ӳ���AC��F����֤��AE=AF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
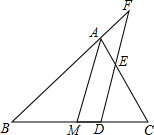 ��ͼ����ABC�У�AMΪBC�������ߣ�DΪBC����һ�㣬��D��DF��AM��AC��E����BA�ӳ�����F����֤��AB��AF=AC��AE��
��ͼ����ABC�У�AMΪBC�������ߣ�DΪBC����һ�㣬��D��DF��AM��AC��E����BA�ӳ�����F����֤��AB��AF=AC��AE���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com