
【题目】如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠ABN,BE的反向延长线与∠BAO的平分线交于点C.
(1)当点A,B移动后,∠BAO=45°时,∠C=________;
(2)当点A,B移动后,∠BAO=60°时,∠C=________;
(3)由(1)(2)猜想∠C是否随点A,B的移动而发生变化,并说明理由.

【答案】(1)(1)45°;(2)45°;(3)∠C不随点A,B的移动而发生变化,理由详见解析.
【解析】
(1)根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠ABN, 再根据角平分线的定义求出∠ABE和∠BAC, 然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解;
(2)与(1)方法相同求解可得答案;
(3)与(1)的思路相同解答可得答案.
解:(1)根据三角形的外角性质,
∠ABN=∠AOB+∠BAO=90![]() +45
+45![]() =135
=135![]()
![]() BE平分∠ABN,AC平分∠BAO,
BE平分∠ABN,AC平分∠BAO,
![]() ∠ABE=
∠ABE=![]() ∠ABN=67.5
∠ABN=67.5![]() ,∠BAC=
,∠BAC=![]() ∠BAO=22.5
∠BAO=22.5![]() ,
,
![]() ∠C=∠ABE-∠BAC=45
∠C=∠ABE-∠BAC=45![]() ,
,
(2)同理:∠ABN=∠AOB+∠BAO=90![]() +60
+60![]() =150
=150![]()
![]() BE平分∠ABN,AC平分∠BAO,
BE平分∠ABN,AC平分∠BAO,
![]() ∠ABE=
∠ABE=![]() ∠ABN=75
∠ABN=75![]() ,∠BAC=
,∠BAC=![]() ∠BAO=30
∠BAO=30![]() ,
,
![]() ∠C=∠ABE-∠BAC=45
∠C=∠ABE-∠BAC=45![]() ,
,
(3)∠C不随点A,B的移动而发生变化.
理由:因为∠ABN是△ABO的外角,
所以∠ABN=∠AOB+∠BAO.
因为BE平分∠ABN,AC平分∠BAO,
所以∠ABE=![]() ∠ABN,∠BAC=
∠ABN,∠BAC=![]() ∠BAO,
∠BAO,
所以∠C=∠ABE-∠BAC=![]() (∠AOB+∠BAO)-
(∠AOB+∠BAO)-![]() ∠BAO=
∠BAO=![]() ∠AOB.
∠AOB.
因为∠AOB=∠MON=90°,
所以∠C=45°.


科目:初中数学 来源: 题型:
【题目】为了拉动内需,广东启动“家电下乡”活动.某家电公司销售给农户的Ⅰ型冰箱和Ⅱ型冰箱在启动活动前一个月共售出980台,启动活动后的第一个月销售给农户的Ⅰ型和Ⅱ型冰箱的销量分别比启动活动前一个月增长30%、25%,这两种型号的冰箱共售出1254台.在启动活动前的一个月,销售给农户的Ⅰ型冰箱和Ⅱ型冰箱分别为多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P,且AE=CF.
(1)求证:AF=BE,并求∠FPB的度数;
(2)若AE=2,试求AP·AF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )

A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,AD是∠BAC的平分线,DE⊥AC于E,DF⊥AB于F,且FB=CE,则下列结论:①DE=DF,②AE=AF,③BD=CD,④AD⊥BC。其中正确的个数有( )

A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组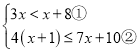 .请结合题意填空,完成本题的解答:
.请结合题意填空,完成本题的解答:
(1)解不等式①,得:________;
(2)解不等式②,得:________;
(3)把不等式①和②的解集在数轴上表示出来:
![]()
(4)原不等式组的解集为:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,∠C=70°,△AB′C′与△ABC 关于直线 EF对称,∠CAF=10°,连接 BB′,则∠ABB′的度数是( )

A. 30° B. 35° C. 40° D. 45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com