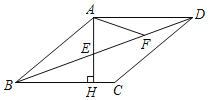
【题目】如图，在菱形ABCD中，过点A作AH⊥BC，分别交BD，BC于点E，H，F为ED的中点，∠BAF＝120°，则∠C的度数为_____．
【答案】140°
【解析】
根据菱形的性质得出AD∥BC，∠ABD＝∠CBD，进而利用三角形的内角和解答即可．
解：设∠CBD＝x，
∵四边形ABCD为菱形，
∴AD∥BC，∠ABD＝∠CBD＝x，
∴∠ADB＝∠CBD＝x，
∵AH⊥BC，AD∥BC，
∴∠DAH＝∠AHB＝90°，
∵F为ED的中点．
∴AF＝FD，
∴∠FAD＝∠ADB＝x，
∵∠BAF＝120°，
∴∠BAD＝120°+x，
∵AD∥BC，
∴∠BAD+∠ABC＝180°，
可得：2x+120°+x＝180°，
解得：x＝20°，
∴∠BAD＝120°+x＝140°
∵四边形ABCD为菱形，
∴∠C＝∠BAD＝140°．
故答案为：140°．
开心蛙口算题卡系列答案科目：初中数学 来源： 题型：
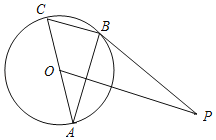
【题目】如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接PB、AB，∠PBA＝∠C．
（1）求证：PB是⊙O的切线；
（2）连接OP，若OP∥BC，且OP＝4，⊙O的半径为
，求BC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
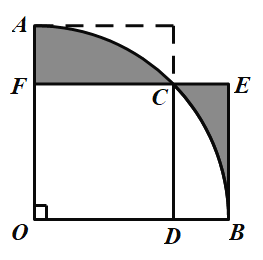
【题目】如图，扇形AOB的圆心角为直角，边长为1的正方形ODCF的顶点F，D，C分别在OA，OB，
上，过点B作BE⊥FC，交FC的延长线于点E，则图中阴影部分的面积等于__．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】学校某数学兴趣小组想测学校旗杆高度如图，明明在稻香园一楼
点测得旗杆顶点
仰角为
，在稻香园二楼
点测得点的仰角为
．明明从点朝旗杆方向步行
米到
点，沿坡度
的台阶走到点
，再向前走
米到旗杆底部
，已知稻香园
高度为
米，则旗杆
的高度约为（ ）（参考数据：
，
，
）
A.
米B.
米C.
米D.
米
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小魏探究学习函数的经验，对函数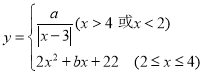
的图像与性质进行了研究，下面是小魏的探究过程，请补充完整．
（1）下表是
与
的几组对应值：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
请直接写出：
_______，
______，
_______．
（2）画出该函数图像．
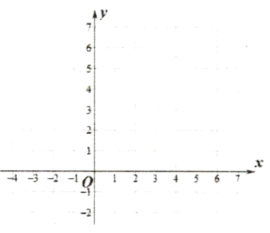
（3）写出该函数的一条性质：_______________．
（4）一次函数
与该函数图像至少有三个交点，则
的范围_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
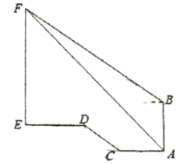
【题目】在△ABC与△ABD中，∠DBA＝∠CAB，AC与BD交于点F
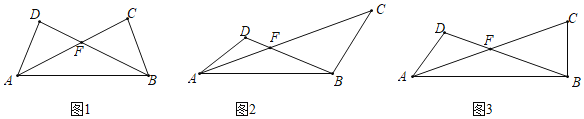
（1）如图1，若∠DAF＝∠CBF，求证：AD＝BC；
（2）如图2，∠D＝135°，∠C＝45°，AD＝2，AC＝4，求BD的长．
（3）如图3，若∠DBA＝18°，∠D＝108°，∠C＝72°，AD＝1，直接写出DB的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知一次函数
的图像与反比例函数
的图像交于点
，与
轴交于点
，若
，且
．
（1）求反比例函数与一次函数的表达式；
（2）若点
为轴上一点，
是等腰三角形，求点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
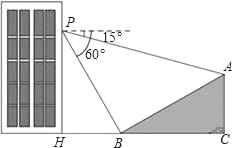
【题目】如图，小明在大楼30米高（即PH＝30米）的窗口P处进行观测，测得山坡上A处的俯角∠APQ为15°，山脚B处的俯角∠BPQ为60°，已知该山坡的坡度i（即tan∠ABC）为1：
，点P，H，B，C，A在同一个平面上，点H、B、C在同一条直线上，且PH丄HC．
（1）求出山坡坡角（∠ABC）的大小；
（2）求A、B两点间的距离（结果精确到0.1米，参考数据：≈1.732）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】广州中学在“读书日”期间购进一批图书， 需要用大小两种规格的纸箱来装运.
个大纸箱和个小纸箱一次可以装
，本书
个大纸箱和
个小纸箱--次可以装
本书．
（1）一个大纸箱和一个小纸箱分别可以装多少本书?
（2）如果一共购入
本书，每个纸箱恰好装满，分别需要用多少个大、小纸箱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
