
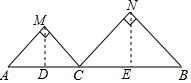
 如图,点C是AB上不与点A、B重合的任意一点,AB=8cn,分别以AC、BC为斜边在AB同侧作等腰直角三角形(△AMC和△CNB),则当BC=4cm时,两个等腰直角三角形的面积和最小.
如图,点C是AB上不与点A、B重合的任意一点,AB=8cn,分别以AC、BC为斜边在AB同侧作等腰直角三角形(△AMC和△CNB),则当BC=4cm时,两个等腰直角三角形的面积和最小. 分析 作MD⊥AC,NE⊥BC,设AC=xcm,则BC=(8-x)cm,将两三角形面积之和表示为S=$\frac{1}{2}$x•$\frac{1}{2}$x+$\frac{1}{2}$•(8-x)•$\frac{1}{2}$(8-x),转化为二次函数的最值问题解答.
解答 解:作MD⊥AC,NE⊥BC,
∵△AMC和△CNB是等腰直角三角形,
∴DC=MD,EB=NE,
∴设AC=xcm,则BC=(8-x)cm,
∴两三角形面积之和为S=$\frac{1}{2}$•x•$\frac{1}{2}$x+$\frac{1}{2}$•(8-x)•$\frac{1}{2}$(8-x)
=$\frac{1}{2}$x2+$\frac{1}{2}$(64+x2-16x)
=$\frac{1}{2}$x2+16+$\frac{1}{2}$x2-4x
=$\frac{1}{2}$x2-4x+16
当AC=-$\frac{-4}{2×\frac{1}{2}}$=4,
即BC=8-4=4cm时,两个等腰三角形的面积最小.
故答案为:4.
点评 本题考查了等腰直角三角形和二次函数的最值,将三角形的面积问题转化为二次函数的最值问题是解题的关键.


科目:初中数学 来源: 题型:选择题
 已知函数y=$\frac{m-1}{x}$(m≠0)的图象如图所示,有以下结论:①m<1;②在每个分支上y随x的增大而增大;③若点A(-2,a),点B(4,b)在图象上,则a<b;④若点P(x,y)在图象上,则点P(-x,-y)也在图象上,则下面选项正确的是( )
已知函数y=$\frac{m-1}{x}$(m≠0)的图象如图所示,有以下结论:①m<1;②在每个分支上y随x的增大而增大;③若点A(-2,a),点B(4,b)在图象上,则a<b;④若点P(x,y)在图象上,则点P(-x,-y)也在图象上,则下面选项正确的是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com