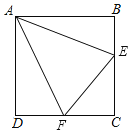
[题目]已知点E.F分别在正方形ABCD的边BC.CD上．若AF平分∠DFE.∠AFE=55°.则∠AEB的度数为( )A.75°B.55°C.80°D.45° 题目和参考答案——青夏教育精英家教网—

【题目】已知点E，F分别在正方形ABCD的边BC，CD上．若AF平分∠DFE，∠AFE=55°，则∠AEB的度数为（　　）

A.75°B.55°C.80°D.45°

【答案】C

【解析】

作AM⊥EF，由题意可证Rt△ABE≌Rt△AEM，可得∠AEB=∠AEF，根据五边形内角和为540°，可求∠BEF=160°，即可求∠AEB的度数．

解：如图：作AM⊥EF

∵四边形ABCD是正方形
∴AB=AD，∠D=∠C=∠B=90°=∠DAB
∵AF平分∠DFE，AD⊥DC，AM⊥EF
∴AD=AM
∵AD=AM，AE=AE
∴Rt△ABE≌Rt△AEM
∴∠AEB=∠AEF
∵∠AFE=55°
∴∠DFE=110°
∵∠B+∠D+∠DAB+∠DFE+∠BEF=540°，
∴∠BEF=160°
∴∠AEB=80°
故选：C.

练习册系列答案

68所名校图书全国著名重点中学3年招生试卷及预测试题精选系列答案

53中考真题卷系列答案

A级口算系列答案

A加优化作业本系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】（1）【问题发现】

如图1，在Rt△ABC中，AB=AC=2，∠BAC=90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，则线段BE与AF的数量关系为　　

（2）【拓展研究】

在（1）的条件下，如果正方形CDEF绕点C旋转，连接BE，CE，AF，线段BE与AF的数量关系有无变化？请仅就图2的情形给出证明；

（3）【问题发现】

当正方形CDEF旋转到B，E，F三点共线时候，直接写出线段AF的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知点E，F在直线AB上，点G在线段CD上，ED与FG交于点H，∠C=∠EFG，∠CED=∠GHD．

（1）求证：CE∥GF；

（2）试判断∠AED与∠D之间的数量关系，并说明理由；

（3）若∠EHF=70°，∠D=30°，求∠AEM的度数．

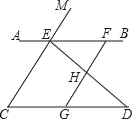
查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】为了尽快的适应中招体考项目，现某校初二（1）班班委会准备筹集1800元购买A、B两种类型跳绳供班级集体使用．

（1）班委会决定，购买A种跳绳的资金不少于B种跳绳资金的2倍，问最多用多少资金购买B种跳绳？

（2）经初步统计，初二（1）班有25人自愿参与购买，那么平均每生需交72元．初三（1）班了解情况后，把体考后闲置的跳绳赠送了若干给初二（1）班，这样只需班级共筹集1350元．经初二（1）班班委会进一步宣传，自愿参与购买的学生在25人的基础上增加了4a%．则每生平均交费在72元基础上减少了2.5a%，求a的值．