
【题目】设二次函数y=ax2+bx﹣(a﹣b)(a,b是常数,a≠0)
(1)判断该二次函数图象与x轴交点的个数,并说明理由;
(2)若该二次函数的图象经过A(﹣1,4),B(0,﹣1),C(1,1)三个点中的其中两个点,求该二次函数的表达式;
(3)若a﹣b<0,点P(﹣2,m)(m>0)在该二次函数图象上,求证:a>0.
【答案】(1)详见解析;(2)y=![]() x2+
x2+![]() x﹣1;(3)详见解析.
x﹣1;(3)详见解析.
【解析】
(1)根据一元二次方程根的判别式分析解答即可;
(2)根据题意先判断抛物线经过点B和点C,然后代入建立二元一次方程组求解可得a和b的值,从而可得二次函数解析式;
(3)把点P代入二次函数解析式,然后根据题意m>0,a-b<0,可求证a>0.
解:(1)∵△=b2﹣4a[﹣(a﹣b)]=b2﹣4ab+4a2=(2a﹣b)2,
当2a=b时,二次函数图象与x轴只有一个交点,
当2a≠b时,二次函数图象与x轴有两个交点;
(2)当x=﹣1时,y=a﹣b﹣(a﹣b)=0,
∴抛物线经过(﹣1,0)和B(0,﹣1),C(1,1),不经过点A(﹣1,4),
把B(0,﹣1),C(1,1)分别代入得:![]() ,
,
解得![]() ,
,
∴抛物线解析式为y=![]() x2+
x2+![]() x﹣1;
x﹣1;
(3)证明:∵点P(﹣2,m)(m>0)在该二次函数图象上,
∴m=a(﹣2)2+(﹣2)b﹣(a﹣b)=3a﹣b,
∵m>0,
∴3a﹣b>0,
∵a﹣b<0,
∴(3a﹣b)﹣(a﹣b)>0,
2a>0,
∴a>0.


科目:初中数学 来源: 题型:
【题目】图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a<0)经过点(-1,0),且满足4a+2b+c>0.以下结论(1)a+b>0;(2)a+c>0;(3)-a+b+c>0;(4)b2-2ac>5a2其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论
①6a﹣b=0;
②abc>0;
③若点M(﹣2,m)与点N(﹣5,n)为抛物线上两点,则m>n;
④ax2+bx+c≥﹣6;
⑤关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1.其中正确结论有( )
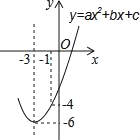
A. 5B. 4C. 3D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,则下面说法正确的是( )
A. 1一定不是方程x2+bx+a=0的根B. 0一定不是方程x2+bx+a=0的根
C. ﹣1可能是方程x2+bx+a=0的根D. 1和﹣1都是方程x2+bx+a=0的根
查看答案和解析>>
科目:初中数学 来源: 题型:
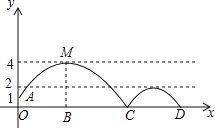
【题目】如图,足球场上守门员在O处踢出一高球,球从离地面1m的A处飞出(A在y轴上),运动员乙在距O点6m的B处发现球在自己头的正上方达到最高点M,距地面有4m高,球落地后又一次弹起,第二个落点为D,据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的解析式;
(2)求足球第一次落地点C处距守门员有多少米?(取![]() ≈1.7)
≈1.7)
(3)运动员乙要抢到第二个落点D处的球,他应再向前跑多少米?(取![]() ≈2.5)
≈2.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
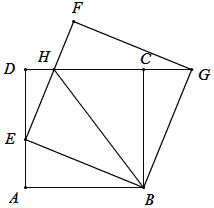
【题目】如图,正方形ABCD的边长为2,点E是AD边上的动点,从点A开始沿AD向D运动.以BE为边,在BE的上方作正方形BEFG,EF交DC于点H,连接CG、BH.请探究:
(1)线段AE与CG是否相等?请说明理由.
(2)若设AE=x,DH=y,当x取何值时,y最大?最大值是多少?
(3)当点E运动到AD的何位置时,△BEH∽△BAE?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冬季,武隆仙女山迎来滑雪季,如图为滑雪场某段赛道示意图,AB段为助滑段,长为12米,坡角α为16°,一个曲面平台BCD连接了助滑坡AB与着陆坡DE,已知着陆坡DE的坡度为i=1:2.4,DE长度为19.5米,B、D之间的垂直距离为5.5米,则一人从A出发到E处下降的垂直距离为( )米(sin16°≈0.28,cos16°≈0.96,tan16°≈0.29,结果保留一位小数)
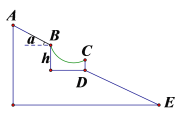
A. 15.9B. 16.4C. 24.5D. 16.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com