
【题目】冬季,武隆仙女山迎来滑雪季,如图为滑雪场某段赛道示意图,AB段为助滑段,长为12米,坡角α为16°,一个曲面平台BCD连接了助滑坡AB与着陆坡DE,已知着陆坡DE的坡度为i=1:2.4,DE长度为19.5米,B、D之间的垂直距离为5.5米,则一人从A出发到E处下降的垂直距离为( )米(sin16°≈0.28,cos16°≈0.96,tan16°≈0.29,结果保留一位小数)
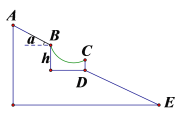
A. 15.9B. 16.4C. 24.5D. 16.0
科目:初中数学 来源: 题型:
【题目】设二次函数y=ax2+bx﹣(a﹣b)(a,b是常数,a≠0)
(1)判断该二次函数图象与x轴交点的个数,并说明理由;
(2)若该二次函数的图象经过A(﹣1,4),B(0,﹣1),C(1,1)三个点中的其中两个点,求该二次函数的表达式;
(3)若a﹣b<0,点P(﹣2,m)(m>0)在该二次函数图象上,求证:a>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=![]() -3x+
-3x+![]() .
.
(1)该二次函数图象与x轴的交点坐标是______;
(2)将y=![]() 化成y=a(x-h)2+k的形式,并写出顶点坐标;
化成y=a(x-h)2+k的形式,并写出顶点坐标;
(3)在坐标轴中画出此抛物线的大致图象;
(4)写出不等式![]() >0的解集.
>0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]()
(1)画出上述二次函数的图象;
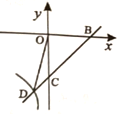
(2)如图,二次函数的图象与x轴的其中一个交点是B,与y轴的交点是C,直线BC与反比例函数的图象交于点D,且BC=3CD,求反比例函数的解析式.
(3)在(2)的条件下,x轴上的点P的横坐标是多少时,△BCP与△OCD相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加,据统计,某小区![]() 年底拥有家庭轿车
年底拥有家庭轿车![]() 辆,
辆,![]() 年底家庭轿车的拥有量达到
年底家庭轿车的拥有量达到![]() 辆.
辆.
(1)若该小区![]() 年底到
年底到![]() 年底家庭轿车拥有量的年平均增长率都相同,求该小区到
年底家庭轿车拥有量的年平均增长率都相同,求该小区到![]() 年底家庭轿车将达到多少辆?
年底家庭轿车将达到多少辆?
(2)为了解决停车困难,该小区决定投资![]() 万元再建造若干个停车位,据测算,室内车位建造费用
万元再建造若干个停车位,据测算,室内车位建造费用![]() 元
元![]() 个,露天车位建造费用
个,露天车位建造费用![]() 元
元![]() 个,考虑到实际因素,计划露天车位的数量不少于室内车位的
个,考虑到实际因素,计划露天车位的数量不少于室内车位的![]() 倍,但不超过室内车位的
倍,但不超过室内车位的![]() 倍,求该小区建造车位共有几种方案?
倍,求该小区建造车位共有几种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“学而时习之,不亦乐乎!”,古人把经常复习当作是一种乐趣,能达到这种境界是非常不容易的。复习可以让遗忘的知识得到补拾,零散的知识变得系统,薄弱的知识有所强化,掌握的知识更加巩固,生疏的技能得到训练。为了了解初一学生每周的复习情况,教务处对初一(1)班学生一周复习的时间进行了调查,复习时间四舍五入后只有4种:1小时,2小时,3小时,4小时,一周复习2小时的女生人数占全班人数的16%,一周复习4小时的男女生人数相等。根据调查结果,制作了两幅不完整的统计图(表):
初一(1)班女生复习时间数据(单位:小时) | |||||||||
0.9 | 1.3 | 1.7 | 1.8 | 1.9 | 2.2 | 2.2 | 2.2 | 2.3 | 2.4 |
3.2 | 3.2 | 3.2 | 3.3 | 3.8 | 3.9 | 3.9 | 4.1 | 4.2 | 4.3 |
女生一周复习时间频数分布表 |
| |
分组(四舍五入)后) | 频数(学生人数) | |
1小时 | 2 | |
2小时 | a | |
3小时 | 4 | |
4小时 | b | |
(1)四舍五入前,女生一周复习时间的众数为 小时,中位数为 小时;
(2)统计图中a = ,c = ,初一(1)班男生人数为 人,根据扇形统计图估算初一(1)班男生的平均复习时间为 小时;
(3)为了激励学生养成良好的复习习惯,教务处决定对一周复习时间四舍五入后达到3小时及以上的全年级学生进行表扬,每人奖励1个笔记本,初一年级共有1000名学生,请问教务处应该准备大约多少个笔记本?
查看答案和解析>>
科目:初中数学 来源: 题型:
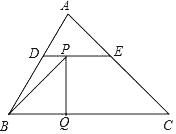
【题目】如图,在△ABC中,∠ABC=60°,∠C=45°,点D,E分别为边AB,AC上的点,且DE∥BC,BD=DE=2,CE=![]() ,BC=
,BC=![]() .动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ⊥BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )
.动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ⊥BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )
A. 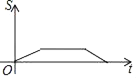 B.
B. 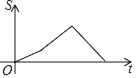
C. 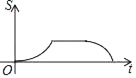 D.
D. 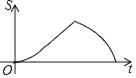
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).
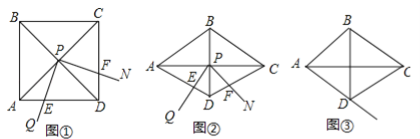
(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是 ;
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF=![]() AD,请给出证明;
AD,请给出证明;
(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,按下任意一个开关均可打开对应的一盏电灯,因刚搬进新房不久,不熟悉情况.
(1)若小明任意按下一个开关,则下列说法正确的是 .
A.小明打开的一定是楼梯灯
B.小明打开的可能是卧室灯
C.小明打开的不可能是客厅灯
D.小明打开走廊灯的概率是![]()
(2)若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图法或列表法加以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com