
【题目】二次函数![]()
(1)画出上述二次函数的图象;
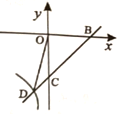
(2)如图,二次函数的图象与x轴的其中一个交点是B,与y轴的交点是C,直线BC与反比例函数的图象交于点D,且BC=3CD,求反比例函数的解析式.
(3)在(2)的条件下,x轴上的点P的横坐标是多少时,△BCP与△OCD相似.
【答案】(1)见解析;(2)![]() ;(3)P的横坐标为5或12时,ΔBCP∽ΔOCD.
;(3)P的横坐标为5或12时,ΔBCP∽ΔOCD.
【解析】
(1)列表,分别取x值代入解析式得出y值,建立坐标系描点,用平滑的曲线连线即可;(2)由(1)可得B、C两点的坐标,过D作DE⊥y轴于E,可证明ΔDEC∽ΔBOC,根据相似三角形的性质可得![]() ,由BC=3CD可求出DE=CE=1,即可求出D点坐标,设反比例函数解析式为y=
,由BC=3CD可求出DE=CE=1,即可求出D点坐标,设反比例函数解析式为y=![]() ,把D点坐标代入求出k值即可得答案;(3)由
,把D点坐标代入求出k值即可得答案;(3)由![]() ,分别讨论
,分别讨论![]() 和
和![]() 两种情况,求出BP的长即可.
两种情况,求出BP的长即可.
(1)①列表
x | … | -1 | 0 | 1 | 2 | 3 | … |
| … | 0 | -3 | -4 | -3 | 0 | … |
②描点;
③连线,
二次函数图象如图所示:
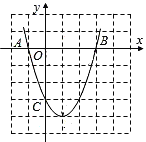
(2)由(1)可知B(3,0)、C(0,-3)
∴OB=OC=3
过D作DE⊥y轴于E
∵∠DCE=∠OCB,∠BOC=∠DEC=90°,
∴ΔDEC∽ΔBOC.
∴![]()
∵BC=3CD
∴DE=CE=1
∴OE=4
∴D(-1,-4)
设反比例函数为![]() ,
,
∴![]() ,即k=4.
,即k=4.
∴反比例函数为![]() .
.
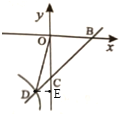
(3)![]()
情况1.![]()
∴![]() ,即BP=9
,即BP=9
∴P(12,0)
情况2.当![]()
∴![]() ,即BP=2
,即BP=2
∴P(5,0)
综合以上两种情况,当P的横坐标为5或12时,ΔBCP∽ΔOCD


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
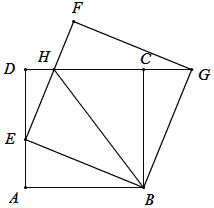
【题目】如图,正方形ABCD的边长为2,点E是AD边上的动点,从点A开始沿AD向D运动.以BE为边,在BE的上方作正方形BEFG,EF交DC于点H,连接CG、BH.请探究:
(1)线段AE与CG是否相等?请说明理由.
(2)若设AE=x,DH=y,当x取何值时,y最大?最大值是多少?
(3)当点E运动到AD的何位置时,△BEH∽△BAE?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AB=4,C为半圆AB的中点,P为![]() 上一动点,延长BP至点Q,使BPBQ=AB2.若点P由A运动到C,则点Q运动的路径长为_____.
上一动点,延长BP至点Q,使BPBQ=AB2.若点P由A运动到C,则点Q运动的路径长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图,则下列说法:①对称轴是直线x=-1;②c=3:③ab>0;④当x<1时,y>0;⑤方程
的部分图象如图,则下列说法:①对称轴是直线x=-1;②c=3:③ab>0;④当x<1时,y>0;⑤方程![]() 的根是
的根是![]() 和
和![]() ,正确的有( )
,正确的有( )

A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,
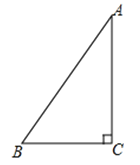
(1)请用直尺和圆规按下列步骤作图(保留作图痕迹),①作![]() 的平分线,交斜边AB于点D;②过点D作AC的垂线,垂足为E.
的平分线,交斜边AB于点D;②过点D作AC的垂线,垂足为E.
(2)在(1)作出的图形中,若![]() ,则DE= .
,则DE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冬季,武隆仙女山迎来滑雪季,如图为滑雪场某段赛道示意图,AB段为助滑段,长为12米,坡角α为16°,一个曲面平台BCD连接了助滑坡AB与着陆坡DE,已知着陆坡DE的坡度为i=1:2.4,DE长度为19.5米,B、D之间的垂直距离为5.5米,则一人从A出发到E处下降的垂直距离为( )米(sin16°≈0.28,cos16°≈0.96,tan16°≈0.29,结果保留一位小数)
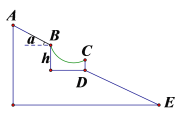
A. 15.9B. 16.4C. 24.5D. 16.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,广场上有一风筝A,小江抓着风筝线的一端站在D处,他从牵引端E测得风筝A的仰角为67°,同一时刻小芸在附近一座距地面30米高(BC=30米)的居民楼顶B处测得风筝A的仰角是45°,已知小江与居民楼的距离CD=40米,牵引端距地面高度DE=1.5米,根据以上条件计算风筝距地面的高度(结果精确到0.1米,参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.414).
≈1.414).
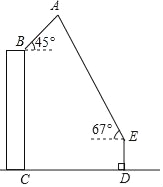
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某校图书馆门前一段笔直的内部道路AB上,过往车辆限速3米/秒在点B的正上方距其7米高的C处有一个探测仪.一辆轿车从点A匀速向点B行驶5秒后此轿车到达D点,探测仪测得∠CAB=18°,∠CDB=45°,求AD之间的距离,并判断此轿车是否超速,(结果精确到0.01米)(参考数据:sinl8°=0.309,cosl8°=0.951,tanl8°=0.325)
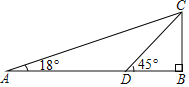
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com