
分析 (1)两位同学的解法均正确;
(2)类比上述方法计算即可;
(3)由以上分母有理化规律,将式子全部有理化后两两抵消可得结果.
解答 解:(1)两位同学的解法均正确;
(2)$\frac{2}{\sqrt{5}-\sqrt{3}}$=$\frac{5-3}{\sqrt{5}-\sqrt{3}}$=$\frac{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}{\sqrt{5}-\sqrt{3}}$=$\sqrt{5}+\sqrt{3}$,
$\frac{2}{\sqrt{5}-\sqrt{3}}=\frac{2(\sqrt{5}+\sqrt{3})}{(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})}$=$\frac{2(\sqrt{5}+\sqrt{3})}{2}=\sqrt{5}+\sqrt{3}$;
(3)原式=$\sqrt{2}-1+\sqrt{3}-\sqrt{2}+\sqrt{4}-\sqrt{3}+\sqrt{5}-\sqrt{4}$+…+$\sqrt{2015}-\sqrt{2014}$
=$\sqrt{2015}-1$.
点评 本题主要考查分母有理化,类比以上分母有理化的方法是解题的根本,将以上方法加以运用是解题的关键.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:填空题
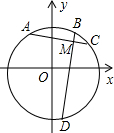 半径为2的圆的圆心O在直角坐标系的原点,两条互相垂直的弦AC和BD相交于点M(1,$\sqrt{2}$),则四边形ABCD的面积的最大值与最小值的差是1.
半径为2的圆的圆心O在直角坐标系的原点,两条互相垂直的弦AC和BD相交于点M(1,$\sqrt{2}$),则四边形ABCD的面积的最大值与最小值的差是1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
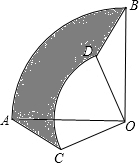 把两个圆心角是90°的扇形OAB与OCD如图那样叠放在一起,连接AC、BD.
把两个圆心角是90°的扇形OAB与OCD如图那样叠放在一起,连接AC、BD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
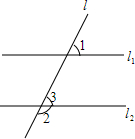 如图,若∠1+∠2=180°,则l1∥l2,试说明理由(填空).
如图,若∠1+∠2=180°,则l1∥l2,试说明理由(填空).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
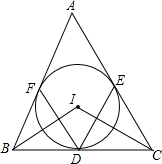 如图,△ABC中,内切圆I和边BC,CA,AB分别相切于点D,F,求证:
如图,△ABC中,内切圆I和边BC,CA,AB分别相切于点D,F,求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com