
【题目】已知:如图,D是△ABC的边BC上的一点,且CD=AB,∠BDA=∠BAD,AE是△ABD的中线.
⑴若∠B=60°,求∠C的值;
⑵求证:AD是∠EAC的平分线.

【答案】(1)∠C=30°;(2)详见解析.
【解析】
(1)根据已知条件得到∠BAD=∠BDA=60°,于是得到AB=AD,等量代换得到CD=AD,根据等腰三角形的性质得到∠DAC=∠C,推出∠BDA=∠DAC+∠C=2∠C,即可得到结论;
(2)证明:延长AE到M,使EM=AE,连接DM,推出△ABE≌△MDE,根据全等三角形的性质得到∠B=∠MDE,AB=DM,根据全等三角形的判定定理得到△MAD≌△CAD,根据全等三角形的性质得到∠MAD=∠CAD于是得到结论.
(1)∵∠B=60°,∠BDA=∠BAD,
∴∠BAD=∠BDA=60°,
∴AB=AD,
∵CD=AB,
∴CD=AD,
∴∠DAC=∠C,
∴∠BDA=∠DAC+∠C=2∠C,
∵∠BAD=60°,
∴∠C=30°;
(2)证明:延长AE到M,使EM=AE,连接DM,

在△ABE和△MDE中,
 ,
,
∴△ABE≌△MDE,
∴∠B=∠MDE,AB=DM,
∵∠ADC=∠B+∠BAD=∠MDE+∠BDA=∠ADM,
在△MAD与△CAD,
 ,
,
∴△MAD≌△CAD,
∴∠MAD=∠CAD,
∴AD是∠EAC的平分线.


科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A.
B.
C.
D.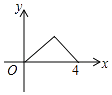
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点P,Q分别在BC,AC上,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下面结论错误的是( )
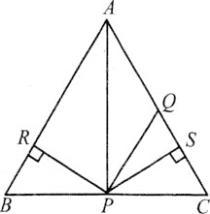
A. ∠BAP=∠CAP B. AS=AR
C. QP∥AB D. △BPR≌△QPS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+c与x轴交于A,B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,﹣3),B(4,0).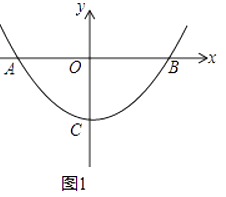
①求该抛物线的解析式;
②若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2)如图2,已知直线PA,PB与y轴分别交于E、F两点.当点P运动时, ![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你用学习“一次函数”时积累的经验和方法研究函数y=|x|的图象和性质,并解决问题.
(1)完成下列步骤,画出函数y=|x|的图象;
①列表、填空;
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 3 | 1 | 1 | 2 | 3 | … |
②描点;
③连线.
(2)观察图象,当x 时,y随x的增大而增大;
(3)根据图象,不等式|x|<![]() x+
x+![]() 的解集为 .
的解集为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,![]() 是直角,OE平分
是直角,OE平分![]() .
.
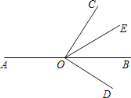
![]() 若
若![]() ,则
,则![]() ______;若
______;若![]() ,则
,则![]() ______;
______;
![]() 若
若![]() ,则
,则![]() ______
______![]() 用含
用含![]() 的式子表示
的式子表示![]() ,请说明理由;
,请说明理由;
![]() 在
在![]() 的内部有一条射线OF,满足
的内部有一条射线OF,满足![]() ,试确定
,试确定![]() 与
与![]() 的度数之间的关系,并说明理由.
的度数之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技与经济的发展,机器人自动化线的市场越来越大,并且逐渐成为自动化生产线的主要方式某化工厂要在规定时间内搬运1800千克化工原料,现有A,B两种机器人可供选择,已知A型机器人每小时完成的工作量是B型机器人的1.5倍,A型机器人单独完成所需的时间比B型机器人少10小时.
(1)求两种机器人每小时分别搬运多少千克化工原料?
(2)若A型机器人工作1小时所需的费用为80元,B型机器人工作1小时所需的费用为60元,若该工厂在两种机器人中选择其中的一种机器人单独完成搬运任务,则选择哪种机器人所需费用较小?请计算说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com