
【题目】请你用学习“一次函数”时积累的经验和方法研究函数y=|x|的图象和性质,并解决问题.
(1)完成下列步骤,画出函数y=|x|的图象;
①列表、填空;
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 3 | 1 | 1 | 2 | 3 | … |
②描点;
③连线.
(2)观察图象,当x 时,y随x的增大而增大;
(3)根据图象,不等式|x|<![]() x+
x+![]() 的解集为 .
的解集为 .

科目:初中数学 来源: 题型:
【题目】2017年4月20日19点41分,天舟一号由长征七号火箭发生升空,经过一天多的飞行,4月22日中午,天舟一号与天宫二号空间实验室进行自动交会对接,形成组合体,某商家根据市场预测,购进“天舟一号”(记作A)、“天宫二号”(记作B)两种航天模型,若购进A种模型10件,B种模型5件,需要1000元;若购进A种模型4件,B种模型3件,需要550元.
(1)求购进A,B两种模型每件需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种模型,考虑到市场需求,要求购进A种模型的数量不超过B种模型数量的8倍,且B种模型最多购进33件,那么该商店共有几种进货方案?
(3)若销售每件A种模型可获利润20元,每件B种模型可获利润30元,在第(2)问的前提下,设销售总盈利为W元,购买B种模型m件,请求出W关于x的函数关系式,并求出当m为何值时,销售总盈利最大,并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角板ABC中,∠ACB=90°,∠B=30°,AC=2 ![]() ,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )
,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( ) 
A.![]() π
π
B.![]() π
π
C.2π
D.3π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,D是△ABC的边BC上的一点,且CD=AB,∠BDA=∠BAD,AE是△ABD的中线.
⑴若∠B=60°,求∠C的值;
⑵求证:AD是∠EAC的平分线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各多少万元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元. 则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查学生对雾霾天气的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了如图所示的不完整的三种统计图表.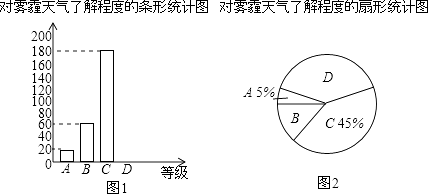
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
A.比较了解 | 15% |
C.基本了解 | 45% |
D.不了解 | n |
请结合统计图表,回答下列问题:
(1)本次参与调查的学生共有人,n=;扇形统计图中D部分扇形所对应的圆心角是度;
(2)请补全条形统计图;
(3)根据调查结果,学校准备开展关于雾霾的知识竞赛,某班要从“非常了解”程度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去,否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区在同一线路上顺次有三个景点A,B,C,甲、乙两名游客从景点A出发,甲步行到景点C;乙花20分钟时间排队后乘观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离景点A的路程s(米)关于时间t(分钟)的函数图像如图所示.
(1)甲的速度是 米/分钟;
(2)当20≤t ≤30时,求乙离景点A的路程s与t的函数表达式;
(3)乙出发后多长时间与甲在途中相遇?
(4)若当甲到达景点C时,乙与景点C的路程为360米,则乙从景点B步行到景点C的速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市先后两次共进货板栗![]() ,进货价依次为10元
,进货价依次为10元![]() 和8元
和8元![]() ,且第二次比第一次多付款800元.
,且第二次比第一次多付款800元.
(1)该超市这两次购进的板栗分别是多少吨?
(2)超市对这![]() 板栗以14元
板栗以14元![]() 的标价销售了
的标价销售了![]() 后,把剩下的板栗全部打折售出,合计获得利润4570元,问超市对剩下的板栗打几折销售?(利润=销售总收入-进货总成本)
后,把剩下的板栗全部打折售出,合计获得利润4570元,问超市对剩下的板栗打几折销售?(利润=销售总收入-进货总成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com