
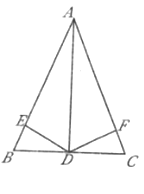
【题目】如图,![]() 是等腰
是等腰![]() 的顶角的平分线,
的顶角的平分线,![]() 点在
点在![]() 上,
上,![]() 点在
点在![]() 上,且
上,且![]() 平分
平分![]() ,则下列结论错误的是 ( )
,则下列结论错误的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
先根据ASA证明△AED≌△AFD,得到AE=AF,DE=DF,∠AED=∠AFD,进而得到BE=FC,∠BED=∠CFD,从而证明△BED≌△CFD,再判断各选项.
∵AD是等腰△ABC的顶角的平分线,AD平分∠EDF,
∴∠DAE=∠DAF,∠EDA=∠FDA,
在△ADE和△ADF中
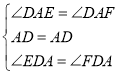 ,
,
∴△ADE≌△ADF(ASA).
∴AE=AF,DE=DF,∠AED=∠AFD,
∴∠BED=∠CFD,
∵△ABC是等腰三角形,
∴AB=AC,
又∵AE=AF,
∴BE=CF,(故A选项正确)
在△BED和△CFD中,
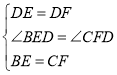 ,
,
∴△BED≌△CFD(SAS),
∴![]() ,
,![]() .(故B、C正确).
.(故B、C正确).
故选:D.


科目:初中数学 来源: 题型:
【题目】某服装店用4000元购进一批某品牌的文化衫若干件,很快售完,该店又用6300元钱购进第二批这种文化衫,所进的件数比第一批多40%,每件文化衫的进价比第一批每件文化衫的进价多10元,请解答下列问题:
(1)求购进的第一批文化衫的件数;
(2)为了取信于顾客,在这两批文化衫的销售中,售价保持了一致.若售完这两批文化衫服装店的总利润不少于4100元钱,那么服装店销售该品牌文化衫每件的最低售价是多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【本小题满分11分】如图,已知抛物线![]() 的顶点D的坐标为(1,
的顶点D的坐标为(1,![]() ),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
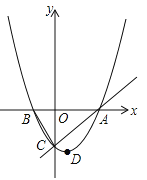
(l)求抛物线所对应的二次函数的表达式;
(2)若动点P满足∠PAO不大于45°,求P点的横坐标m的取值范围;
(3)当P点的横坐标![]() 时,过p点作y轴的垂线PQ,垂足为Q.问:是否存在P点,使∠QPO=∠BCO?若存在,请求出P点的坐标;若不存在,请说明理由.
时,过p点作y轴的垂线PQ,垂足为Q.问:是否存在P点,使∠QPO=∠BCO?若存在,请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x+m)2的顶点坐标为(﹣1,0),且过点A(﹣2,﹣![]() ).
).
(1)求这个二次函数的解析式;
(2)点B(2,﹣2)在这个函数图象上吗?
(3)你能通过左,右平移函数图象,使它过点B吗?若能,请写出平移方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数 y kx 与 y  的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数
的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数 的图象于点 C,连接 BC,则△ABC 的面积为( )
的图象于点 C,连接 BC,则△ABC 的面积为( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
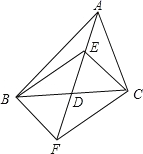
【题目】在△ABC 中,D 是 BC 边的中点,E、F 分别在 AD 及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF ≌△CDE;
(2)若 DE = BC,试判断四边形 BFCE 是怎样的四边形,并证明你的结论.
BC,试判断四边形 BFCE 是怎样的四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
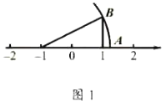
【题目】(1)如图1,![]() 中,
中,![]() ,点
,点![]() 在数轴-1处,点
在数轴-1处,点![]() 在数轴1处,
在数轴1处,![]() ,
,![]() ,则数轴上点
,则数轴上点![]() 对应的数是 .
对应的数是 .
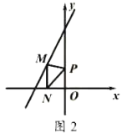
(2)如图2,点![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,点
,点![]() 是
是![]() 轴上的动点,当以
轴上的动点,当以![]() ,
,![]() ,
,![]() 为顶点的三角形为等腰直角三角形时点
为顶点的三角形为等腰直角三角形时点![]() 的坐标为 .
的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师所留的作业中有这样一个分式的计算题:![]() ,甲、乙两位同学完成的过程分别如下:
,甲、乙两位同学完成的过程分别如下:
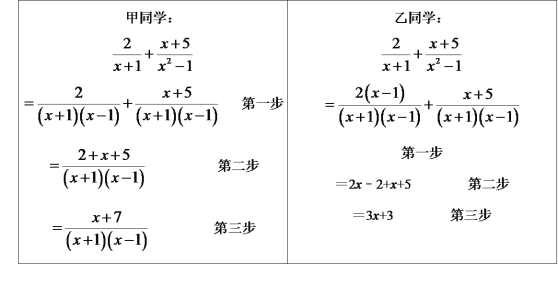
老师发现这两位同学的解答都有错误.
请你从甲、乙两位同学中,选择一位同学的解答过程,帮助他分析错因,并加以改正.
(1)我选择 同学的解答过程进行分析.(填“甲”或“乙”)该同学的解答从第 步开始出现错误,错误的原因是 ;
(2)请重新写出完成此题的正确解答过程.
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com