
【题目】如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?

【答案】3cm.
【解析】
试题根据矩形的性质得AB=CD=8,BC=AD=10,∠B=∠C=90°,再根据折叠的性质得AF=AD=10,DE=EF,在Rt△ABF中,利用勾股定理计算出BF=6,则CF=BC﹣BF=4,设CE=x,则DE=EF=8﹣x,在Rt△CEF中利用勾股定理得到∴42+x2=(8﹣x)2,然后解方程即可.
试题解析:∵四边形ABCD为矩形,∴AB=CD=8,BC=AD=10,∠B=∠C=90°.
∵长方形纸片ABCD折纸,顶点D落在BC边上的点F处(折痕为AE),
∴AF=AD=10,DE=EF,
在Rt△ABF中,AB=8,AF=10,∴BF=![]() .
.
∴CF=BC﹣BF=4.
设CE=x,则DE=EF=8﹣x,
在Rt△CEF中,∵CF2+CE2=EF2,
∴42+x2=(8﹣x)2,解得x=3.
∴EC的长为3cm.


科目:初中数学 来源: 题型:
【题目】综合题:探索发现
(1)自主阅读:在三角形的学习过程,我们知道三角形一边上的中线将三角形分成了两个面积相等三角形,原因是两个三角形的底边和底边上的高都相等,在此基础上我们可以继续研究:如图1,AD∥BC,连接AB,AC,BD,CD,则S△ABC=S△BCD .
证明:分别过点A和D,作AF⊥BC于F.DE⊥BC于E,由AD∥BC,可得AF=DE,又因为S△ABC= ![]() ×BC×AF,S△BCD=
×BC×AF,S△BCD= ![]() .
.
所以S△ABC=S△BCD
由此我们可以得到以下的结论:像图1这样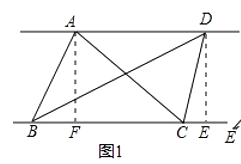
(2)问题解决:如图2,四边形ABCD中,AB∥DC,连接AC,过点B作BE∥AC,交DC延长线于点E,连接点A和DE的中点P,请你运用上面的结论证明:SABCD=S△APD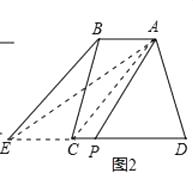
(3)应用拓展:
如图3,按此方式将大小不同的两个正方形放在一起,连接AF,CF,若大正方形的面积是80cm2 , 则图中阴影三角形的面积是cm2 . 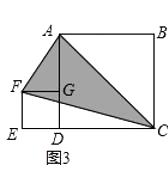
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种树苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.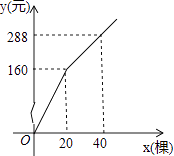
(1)求y与x的函数关系式;
(2)若在购买计划中,B种树苗的数量不超过35棵,但不少于A种树苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和直尺画图:
(1)补全△A′B′C′;
(2)作出△ABC的中线CD;
(3)画出BC边上的高线AE;
(4)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有 个.(注:格点指网格线的交点)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车油箱内有油a升,从某地出发,每行驶1小时耗油6升,若设剩余油量为Q升,行驶时间为t/小时,根据以上信息回答下列问题:
(1)开始时,汽车的油量a=_____升;
(2)在_____小时汽车加油,加了_____升,
写出加油前Q与t之间的关系式______;
(3)这辆汽车行驶8小时,剩余油量多少升?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com