
【题目】综合题:探索发现
(1)自主阅读:在三角形的学习过程,我们知道三角形一边上的中线将三角形分成了两个面积相等三角形,原因是两个三角形的底边和底边上的高都相等,在此基础上我们可以继续研究:如图1,AD∥BC,连接AB,AC,BD,CD,则S△ABC=S△BCD .
证明:分别过点A和D,作AF⊥BC于F.DE⊥BC于E,由AD∥BC,可得AF=DE,又因为S△ABC= ![]() ×BC×AF,S△BCD=
×BC×AF,S△BCD= ![]() .
.
所以S△ABC=S△BCD
由此我们可以得到以下的结论:像图1这样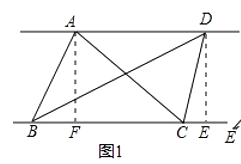
(2)问题解决:如图2,四边形ABCD中,AB∥DC,连接AC,过点B作BE∥AC,交DC延长线于点E,连接点A和DE的中点P,请你运用上面的结论证明:SABCD=S△APD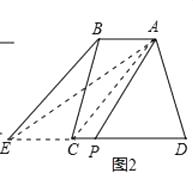
(3)应用拓展:
如图3,按此方式将大小不同的两个正方形放在一起,连接AF,CF,若大正方形的面积是80cm2 , 则图中阴影三角形的面积是cm2 . 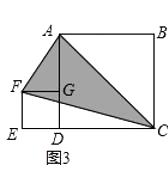
【答案】
(1)同底等高的两三角形面积相等
(2)证明:∵AB∥CE,BE∥AC,
∴四边形ABEC为平行四边形,
∴△ABC和△AEC的公共边AC上的高也相等,
∴S△ABC=S△AEC,
∴S梯形ABCD=S△ACD+S△ABC=S△ACD+S△AEC=S△AED
(3)40
【解析】解;(1)利用图形直接得出:同底等高的两三角形面积相等;
所以答案是:同底等高的两三角形面积相等;(3)设正方形ABCD的边长为a,正方形DGFE的边长为b,
∵S△ACF=S四边形ACEF﹣S△CEF=S△AFG+S正方形DEFG+S△ADC﹣S△CEF= ![]() ×b×(a﹣b)+b×b+
×b×(a﹣b)+b×b+ ![]() ×a×a﹣
×a×a﹣ ![]() ×b×(b+a)=
×b×(b+a)= ![]() ab﹣
ab﹣ ![]() b2+b2+
b2+b2+ ![]() a2﹣
a2﹣ ![]() b2﹣
b2﹣ ![]() ab=
ab= ![]() a2,
a2,
∴S△ACF= ![]() S正方形ABCD=
S正方形ABCD= ![]() ×80cm2=40cm2;
×80cm2=40cm2;
所以答案是:40.
【考点精析】掌握三角形的面积和平行四边形的性质是解答本题的根本,需要知道三角形的面积=1/2×底×高;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


科目:初中数学 来源: 题型:
【题目】(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a、b的式子表示);
(2)应用:点A为线段BC外一动点,且BC=4,AB=2,如图2,分别以AB、AC为边,作等边三角形ABD和等边△ACE,连接CD、BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值;
③直接写出△DBC面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交车每月的支出费用为4000元,票价为2元/人,设每月有![]() 人乘坐该公交车,每月利润为
人乘坐该公交车,每月利润为![]() 元(利润=收入-支出).
元(利润=收入-支出).
(1)请写出![]() 与
与![]() 的关系式 ;
的关系式 ;
(2)完成表格.
| 500 | 1000 | 1500 | 2000 | 2500 | 3000 | … |
|
|
|
|
|
|
| … |
(3)观察表中数据,每月乘客量达到 人以上时,该公交车才不会亏损.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y= ![]() (x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
(x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.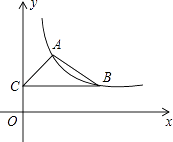
(1)求该反比例函数解析式;
(2)当△ABC面积为2时,求点B的坐标.
(3)P为线段AB上一动点(P不与A、B重合),在(2)的情况下,直线y=ax﹣1与线段AB交于点P,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明准备测量一段水渠的深度,他把一根竹竿AB竖直插到水底,此时竹竿AB离岸边点C处的距离![]() 米。竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )
米。竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )

A. 2米B. 2.5米C. 2.25米D. 3米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】3月5日是学雷锋日,某校组织了以“向雷锋同志学习”为主题的小报制作比赛,评分结果只有60,70,80,90,100五种.现从中随机抽取部分作品,对其份数及成绩进行整理,制成如下两幅不完整的统计图.根据以下信息,解答下列问题: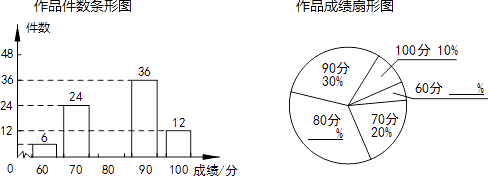
(1)求本次抽取了多少份作品,并补全两幅统计图;
(2)已知该校收到参赛作品共1200份,请估计该校学生比赛成绩达到90分以上(含90分)的作品有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABC中,AB=AC,点E在CA的延长线上,EP⊥BC,垂足为P,EP交AB于点F,FD∥AC交BC于点D.求证:△AEF是等腰三角形.
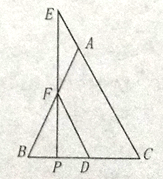
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com