
【题目】某公交车每月的支出费用为4000元,票价为2元/人,设每月有![]() 人乘坐该公交车,每月利润为
人乘坐该公交车,每月利润为![]() 元(利润=收入-支出).
元(利润=收入-支出).
(1)请写出![]() 与
与![]() 的关系式 ;
的关系式 ;
(2)完成表格.
| 500 | 1000 | 1500 | 2000 | 2500 | 3000 | … |
|
|
|
|
|
|
| … |
(3)观察表中数据,每月乘客量达到 人以上时,该公交车才不会亏损.
【答案】(1)y=2x-4000; (2)见解析表格;(3)2000
【解析】
(1)由于公交车每月的支出费用为4000元,票价为2元/人次,设每月有x人乘坐该公交车,每月利润为![]() 元(利润=收入-支出),由此可以列出y与x之间的关系式;
元(利润=收入-支出),由此可以列出y与x之间的关系式;
(2)分别把所给数据代入![]() 与
与![]() 的关系式计算即可求解;
的关系式计算即可求解;
(3)根据计算结果可以直接得到结论.
解:(1)依题意得,
y=2x-4000;
(2)完成表格.
x人 | 500 | 1000 | 1500 | 2000 | 2500 | 3000 |
y元 | -3000 | -2000 | -1000 | 0 | 1000 | 2000 |
(3)根据表格可知,当每月乘客量达到2000人以上时,收入大于支出,该公交车才不会亏损.
故答案为:(1)y=2x-4000; (2)见解析表格;(3)2000.


科目:初中数学 来源: 题型:
【题目】如图,折线ABCDE描述了一辆汽车在某一直线上行驶过程中,汽车离出发地的距离y(km)和行驶时间x(h)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120km;②汽车在行驶途中停留了0.5h;③汽车在整个行驶过程中的平均速度为![]() km/h;④汽车自出发后3h~4.5h之间行驶的速度在逐渐减小.其中正确的说法是 .(填上所有正确的序号)
km/h;④汽车自出发后3h~4.5h之间行驶的速度在逐渐减小.其中正确的说法是 .(填上所有正确的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.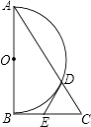
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在《科学》课上,老师讲到温度计的使用方法及液体的沸点时,好奇的王红同学准备测量食用油的沸点,已知食用油的沸点温度高于水的沸点温度(![]() ),王红家只有刻度不超过
),王红家只有刻度不超过![]() 的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔
的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔![]() 测量一次锅中油温,测量得到的数据如下表:
测量一次锅中油温,测量得到的数据如下表:
时间 | 0 | 10 | 20 | 30 | 40 |
油温 | 10 | 30 | 50 | 70 | 90 |
王红发现,烧了![]() 时,油沸腾了,则下列说法不正确的是( )
时,油沸腾了,则下列说法不正确的是( )
A. 没有加热时,油的温度是![]()
B. 加热![]() ,油的温度是
,油的温度是![]()
C. 估计这种食用油的沸点温度约是![]()
D. 每加热![]() ,油的温度升高
,油的温度升高![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
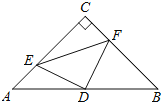
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,D是AB的中点,点E、F分别在AC、BC边上运动
,D是AB的中点,点E、F分别在AC、BC边上运动![]() 点E不与点A、C重合
点E不与点A、C重合![]() ,且保持
,且保持![]() ,连接DE、DF、
,连接DE、DF、![]() 在此运动变化的过程中,有下列结论:
在此运动变化的过程中,有下列结论:![]() ;
;![]() 四边形CEDF的面积随点E、F位置的改变而发生变化;
四边形CEDF的面积随点E、F位置的改变而发生变化;![]() ;
;![]() 以上结论正确的是______
以上结论正确的是______![]() 只填序号
只填序号![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题:探索发现
(1)自主阅读:在三角形的学习过程,我们知道三角形一边上的中线将三角形分成了两个面积相等三角形,原因是两个三角形的底边和底边上的高都相等,在此基础上我们可以继续研究:如图1,AD∥BC,连接AB,AC,BD,CD,则S△ABC=S△BCD .
证明:分别过点A和D,作AF⊥BC于F.DE⊥BC于E,由AD∥BC,可得AF=DE,又因为S△ABC= ![]() ×BC×AF,S△BCD=
×BC×AF,S△BCD= ![]() .
.
所以S△ABC=S△BCD
由此我们可以得到以下的结论:像图1这样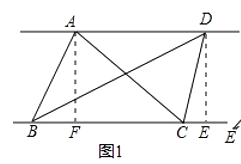
(2)问题解决:如图2,四边形ABCD中,AB∥DC,连接AC,过点B作BE∥AC,交DC延长线于点E,连接点A和DE的中点P,请你运用上面的结论证明:SABCD=S△APD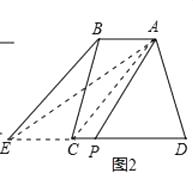
(3)应用拓展:
如图3,按此方式将大小不同的两个正方形放在一起,连接AF,CF,若大正方形的面积是80cm2 , 则图中阴影三角形的面积是cm2 . 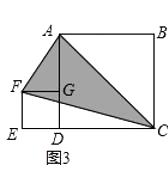
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com