
����Ŀ��(1)���֣���ͼ1����AΪ�߶�BC��һ���㣬��BC��a��AB��b��
��գ�����Aλ���� ��ʱ���߶�AC�ij�ȡ�����ֵ�������ֵΪ�� ��(�ú�a��b��ʽ�ӱ�ʾ)��
(2)Ӧ�ã���AΪ�߶�BC��һ���㣬��BC��4��AB��2����ͼ2���ֱ���AB��ACΪ�ߣ����ȱ�������ABD�͵ȱߡ�ACE������CD��BE��
�����ҳ�ͼ����BE��ȵ��߶Σ���˵�����ɣ�
��ֱ��д���߶�BE�������ֵ��
��ֱ��д����DBC��������ֵ��

���𰸡�(1)CB���ӳ����ϣ�a+b��(2)��CD��BE�����ɼ���������6����4.
��������
��1�����ݵ�Aλ��CB���ӳ�����ʱ���߶�AC�ij�ȡ�����ֵ�����ɵõ����ۣ�
��2���ٸ��ݵȱ������ε����ʵõ�AD��AB��AC��AE����BAD����CAE��60�����Ƴ���CAD�ա�EAB������ȫ�������ε����ʵõ�CD��BE��
�������߶�BE�������ֵ���߶�CD�����ֵ�����ݣ�1���еĽ��ۼ��ɵõ������
����DP��CB����CB�ӳ����ڵ�P����DB��BCʱ��DPȡ�����ֵ�����ֵΪ2���ٸ��������ε������ʽ���ɵã�
(1)�ߵ�AΪ�߶�BC��һ���㣬��BC��a��AB��b��
�൱��Aλ��CB���ӳ�����ʱ���߶�AC�ij�ȡ�����ֵ�������ֵΪBC+AB��a+b��
�ʴ�Ϊ��CB���ӳ����ϣ�a+b��
(2)��CD��BE��
���ɣ��ߡ�ABD����ACE�ǵȱ������Σ�
��AD��AB��AC��AE����BAD����CAE��60����
���BAD+��BAC����CAE+��BAC��
����CAD����EAB��
����CAD����EAB��
��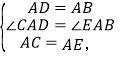
���CAD�ա�EAB(SAS)��
��CD��BE��
�ڡ��߶�BE�������ֵ���߶�CD�����ֵ��
��(1)֪�����߶�CD�ij�ȡ�����ֵʱ����D��CB���ӳ����ϣ�
�����ֵΪBD+BC��AB+BC��6��
����ͼ������D��DP��CB����CB�ӳ����ڵ�P��
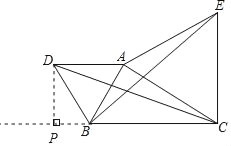
��Rt��BDP��DP��DB��
��DB��BCʱ��DPȡ�����ֵ�����ֵΪ2��
���DBC��������ֵΪ![]()


 ���ʿ��ÿ��ֳɳ�ϵ�д�
���ʿ��ÿ��ֳɳ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�BFƽ�֡�ABC����AD�ڵ�F��CEƽ�֡�BCD����AD�ڵ�E��AB=7��EF=3����BC��Ϊ�� ��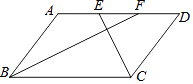
A.9
B.10
C.11
D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCDE������һ��������ijһֱ������ʻ�����У�����������صľ���y(km)����ʻʱ��x(h)֮��ĺ�����ϵ������ͼ���ṩ����Ϣ����������˵��������������ʻ��120km������������ʻ;��ͣ����0.5h����������������ʻ�����е�ƽ���ٶ�Ϊ![]() km/h���������Գ�����3h��4.5h֮����ʻ���ٶ�����С��������ȷ��˵���� .������������ȷ����ţ�
km/h���������Գ�����3h��4.5h֮����ʻ���ٶ�����С��������ȷ��˵���� .������������ȷ����ţ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
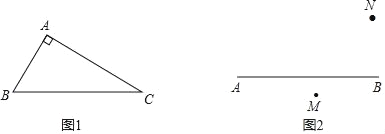
����Ŀ��(1)��ͼ1����Rt��ABC�У�AB��3��AC��4��BC��5����ֱ��EF��ֱƽ��BC���������ó߹滭��ֱ��EF��
(2)����P��(1)��BC�Ĵ�ֱƽ����EF�ϣ���ֱ��д��PA+PB����Сֵ���ش�PA+PBȡ��Сֵʱ��P��λ�ò���ͼ�б������
�⣺PA+PB����СֵΪ�� ����PA+PBȡ��Сֵʱ��P��λ������ ����
(3)��ͼ2����M��N�ֱ���ֱ��AB���࣬��ֱ��AB����һ��Q��ʹ�á�MQB����NQB��Ҫ��ͼ������Ҫ����ȷ����Qλ�õIJ���(����߹���ͼ��������ͼ�ۼ�������֤��)
�⣺ȷ����Qλ�õļ�Ҫ���裺�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A(1��2)��B(3��1)��C(��2����1)
(1)��ͼ��������ABC����y��ԳƵġ�A1B1C1��
(2)д��A1��B1��C1�����ꣻ
(3)���A1B1C1�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
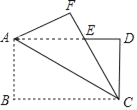
����Ŀ����ͼ����������ABCD�ضԽ���AC���ۣ���B���ڵ�F����FC��AD�ڵ�E����AB=4��BC��8������ACE�����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���ABC=90�㣬��ABΪֱ������Բ��O��AC���D����EΪBC���е㣬����DE��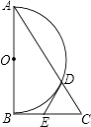
��1����֤��DE�ǰ�Բ��O�����ߣ�
��2������BAC=30�㣬DE=2����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ��⣺̽������
��1�������Ķ����������ε�ѧϰ���̣�����֪��������һ���ϵ����߽������ηֳ������������������Σ�ԭ�������������εĵױߺ͵ױ��ϵĸ߶���ȣ��ڴ˻��������ǿ��Լ����о�����ͼ1��AD��BC������AB��AC��BD��CD����S��ABC=S��BCD ��
֤�����ֱ����A��D����AF��BC��F��DE��BC��E����AD��BC���ɵ�AF=DE������ΪS��ABC= ![]() ��BC��AF��S��BCD=
��BC��AF��S��BCD= ![]() ��
��
����S��ABC=S��BCD
�ɴ����ǿ��Եõ����µĽ��ۣ���ͼ1����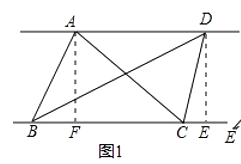
��2������������ͼ2���ı���ABCD�У�AB��DC������AC������B��BE��AC����DC�ӳ����ڵ�E�����ӵ�A��DE���е�P��������������Ľ���֤����SABCD=S��APD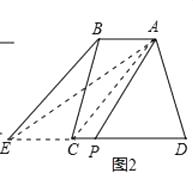
��3��Ӧ����չ��
��ͼ3�����˷�ʽ����С��ͬ�����������η���һ������AF��CF�����������ε������80cm2 �� ��ͼ����Ӱ�����ε������cm2 �� 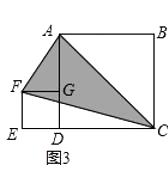
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com