
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于点D,下列四个结论:①BE=EF-CF;②∠BOC=90°+![]() ∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=
∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=![]() mn,其中正确的结论是______.(填所有正确的序号)
mn,其中正确的结论是______.(填所有正确的序号)

【答案】①②③④
【解析】
由在△ABC中,∠ABC和∠ACB的平分线相交于点O,根据角平分线的定义与三角形内角和定理,即可求得②∠BOC=90°+![]() ∠A正确;由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出BE=EF-CF故①正确;由角平分线的性质得出点O到△ABC各边的距离相等,故③正确;由角平分线定理与三角形面积的求解方法,即可求得③设OD=m,AE+AF=n,则S△AEF=
∠A正确;由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出BE=EF-CF故①正确;由角平分线的性质得出点O到△ABC各边的距离相等,故③正确;由角平分线定理与三角形面积的求解方法,即可求得③设OD=m,AE+AF=n,则S△AEF=![]() mn,故④正确.
mn,故④正确.
解:∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∠A+∠ABC+∠ACB=180°,
∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°-![]() ∠A,
∠A,
∴∠BOC=180°-(∠OBC+∠OCB)=90°+![]() ∠A;故②正确;
∠A;故②正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
即BE=EF-CF.故①正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,
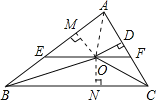
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,
∴S△AEF=S△AOE+S△AOF=![]() AEOM+
AEOM+![]() AFOD=
AFOD=![]() OD(AE+AF)=
OD(AE+AF)=![]() mn;故④正确;
mn;故④正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴点O到△ABC各边的距离相等,故③正确.
故答案为①②③④.


科目:初中数学 来源: 题型:
【题目】九年级某班同学在庆祝2015年元旦晚会上进行抽奖活动.在一个不透明的口袋中有三个完全相同的小球,把它们分别标号1、2、3.随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号.
(1)请用列表或画树形图的方法(只选其中一种),表示两次摸出小球上的标号的所有结果;
(2)规定当两次摸出的小球标号相同时中奖,求中奖的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王伟准备用一段长30米的篱笆围成一个三角形形状的小圈,用于饲养家兔.已知第一条边长为a米,由于受地势限制,第二条边长只能是第一条边长的2倍多2米.
(1)请用a表示第三条边长;
(2)问第一条边长可以为7米吗?请说明理由,并求出a的取值范围;
(3)能否使得围成的小圈是直角三角形形状,且各边长均为整数?若能,说明你的围法;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
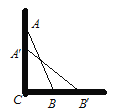
【题目】一架长2.5米的梯子AB如图所示斜靠在一面墙上,这时梯足B离墙底C(∠C=90°)的距离BC为0.7米.
(1)求此时梯顶A距地面的高度AC;
(2)如果梯顶A下滑0.9米,那么梯足B在水平方向,向右滑动了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),我们把点![]() (-y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(2,4),点A2017的坐标为 ( )
(-y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(2,4),点A2017的坐标为 ( )
A. (-3,3) B. (-2,-2) C. (3,-1) D. (2,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把100个纸杯整齐叠放在一起时,它的高度约是( )

A.106cmB.110cmC.114cmD.116cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=![]() , BC=2,以AB
, BC=2,以AB![]() 为直径的⊙O分别交AC、BC于点D、E。
为直径的⊙O分别交AC、BC于点D、E。
(1)求证:E是BC的中点;
(2)连结DE,求证:△CDE∽△CBA;
(3)求△CDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1):
(1)请画出△ABC沿![]() 轴向右平移3个单位长度,再沿
轴向右平移3个单位长度,再沿![]() 轴向上平移2个单位长度后的
轴向上平移2个单位长度后的![]() (其中
(其中![]() 分别是A、B、C的对应点,不写画法);
分别是A、B、C的对应点,不写画法);
(2)直接写出![]() 三点的坐标;
三点的坐标;
(3)求△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com