
某酒厂生产A、B两种品牌的酒,每天两种酒共生产600瓶,每种酒每瓶的成本和利润如下表所示.设每天共获利y元,每天生产A种品牌的酒x瓶.
| A | B | |
| 成本(元) | 50 | 35 |
| 利润(元) | 20 | 15 |
(1)请写出y关于x的函数关系式;
(2)如果该厂每天至少投入成本25000元,且生产B种品牌的酒不少于全天产量的55%,那么共有几种生产方案?并求出每天至少获利多少元?
【考点】一次函数的应用.
【分析】(1)根据获利y=A种品牌的酒的获利+B种品牌的酒的获利,即可解答.
(2)根据生产B种品牌的酒不少于全天产量的55%,A种品牌的酒的成本+B种品牌的酒的成本≥25000,列出方程组,求出x的取值范围,根据x为正整数,即可得到生产方案;再根据一次函数的性质,即可求出每天至少获利多少元.
【解答】解:(1)由题意,每天生产A种品牌的酒x瓶,则每天生产B种品牌的酒(600﹣x)瓶,
∴y=20x+15(600﹣x)=9000+5x.
(2)根据题意得: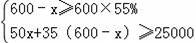
 ,
,
解得:266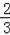
 ≤x≤270,
≤x≤270,
∵x为整数,
∴x=267、268、269、270,
该酒厂共有4种生产方案:
①生产A种品牌的酒267瓶,B种品牌的酒333瓶;
②生产A种品牌的酒268瓶,B种品牌的酒332瓶;
③生产A种品牌的酒269瓶,B种品牌的酒331瓶;
④生产A种品牌的酒270瓶,B种品牌的酒330瓶;
∵每天获利y=9000+5x,y是关于x的一次函数,且随x的增大而增大,
∴当x=267时,y有最小值,y最小=9000+5×267=10335元.
【点评】本题考查了一次函数的应用,关键从表格种获得成本价和利润,然后根据利润这个等量关系列解析式,根据第二问中的利润和成本做为不等量关系列不等式组分别求出解,然后根据一次函数的性质求出哪种方案获利最小.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:
如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )


A.∠AED=∠B B.∠ADE=∠C C.
 =
=
 D.
D.
 =
=

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P.
(1)求证:AP是⊙O的切线;
(2)OC=CP,AB=6,求CD的长.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com