
分析 (1)由分式的分子恒大于0,分式的值为正数,得到分母大于0,即可求出x的范围;
(2)由分式的分母恒大于0,分式的值为负数,得到分子小于0,即可求出x的范围;
(3)根据分式的值为-1且分母不为0列出不等式组求解即可.
解答 解:(1)∵分式$\frac{4}{6-x}$的值为正,
∴6-x>0,
∴x<6;
故答案为:<6;
(2)∵分式$\frac{1-x}{2{x}^{2}+1}$的值为负,
∴1-x<0,
∴x>1,
故答案为:>1;
(3)∵分式的值为-1,
∴$\frac{x+2}{|x|-2}$=-1.
分式两边同时乘以|x|-2得:x+2=2-|x|.
移项得:|x|+x=0.
∴x≤0.
∵分式的分母不为0,
∴|x|-2≠0.
解得:x≠±2.
∴x的取值范围是x≤0且x≠-2.
故答案为:x≤0且x≠-2.
点评 此题考查了分式的值,以及分式有意义的条件,是一道基本题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
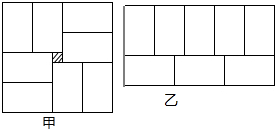
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
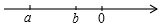 已知实数a、b在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$+|a+b|+|$\sqrt{2}$-a|-$\sqrt{(b-\sqrt{2})^{2}}$.
已知实数a、b在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$+|a+b|+|$\sqrt{2}$-a|-$\sqrt{(b-\sqrt{2})^{2}}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
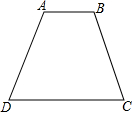 如图,在等腰梯形ABCD中,AB∥CD,AD=BC=6,点P在线段AD上,满足条件∠BPC=90°的点P有且只有一个,则等腰梯形ABCD的面积是18.
如图,在等腰梯形ABCD中,AB∥CD,AD=BC=6,点P在线段AD上,满足条件∠BPC=90°的点P有且只有一个,则等腰梯形ABCD的面积是18.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
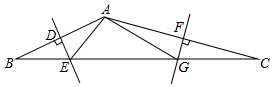 如图,△ABC中,BC=7,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.则△AEG的周长为7.
如图,△ABC中,BC=7,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.则△AEG的周长为7.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
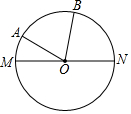 在半径为1的⊙O中,MN是直径,∠AOM=27°,∠BOA=66°,在直径MN上有一点C,AC+BC的和最小,则这个最小值等于$\sqrt{3}$.
在半径为1的⊙O中,MN是直径,∠AOM=27°,∠BOA=66°,在直径MN上有一点C,AC+BC的和最小,则这个最小值等于$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12×106 | B. | 1.2×106 | C. | 1.2×107 | D. | 1.2×108 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com