
分析 利用完全平方公式变形得到原式=$\frac{2}{\sqrt{(\sqrt{10}-\sqrt{2})^{2}}}$-$\frac{1}{\frac{\sqrt{(\sqrt{3}+\sqrt{2})^{2}}}{\sqrt{2}}}$,然后利用二次根式的性质化简后进行分母有理化即可.
解答 解:原式=$\frac{2}{\sqrt{12-2\sqrt{20}}}$-$\frac{1}{\sqrt{\frac{6+2\sqrt{5}}{2}}}$
=$\frac{2}{\sqrt{(\sqrt{10}-\sqrt{2})^{2}}}$-$\frac{1}{\frac{\sqrt{(\sqrt{3}+\sqrt{2})^{2}}}{\sqrt{2}}}$
=$\frac{2}{\sqrt{10}-\sqrt{2}}$-$\frac{\sqrt{2}}{\sqrt{3}+\sqrt{2}}$
=$\frac{\sqrt{2}}{\sqrt{5}-1}$-$\sqrt{2}$($\sqrt{3}$-$\sqrt{2}$)
=$\frac{\sqrt{10}}{4}$-$\frac{\sqrt{2}}{4}$-$\sqrt{6}$+2.
故答案为$\frac{\sqrt{10}}{4}$-$\frac{\sqrt{2}}{4}$-$\sqrt{6}$+2.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
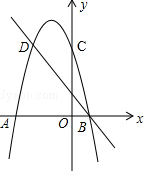 如图,二次函数y=-x2-2x+3的图象与x轴交于A和B两点(A在B左边),交y轴于点C,C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数y=-x2-2x+3的图象与x轴交于A和B两点(A在B左边),交y轴于点C,C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| R(cm) | 1 | 2 | 3 | 4 | 5 | 6 |
| h(cm) | $\frac{50}{π}$ | $\frac{25}{2π}$ | $\frac{50}{9π}$ | $\frac{25}{8π}$ | $\frac{2}{π}$ | $\frac{25}{8π}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
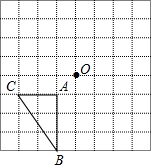 如图所示,△ABC的顶点与点O在8×8的网格中的格点上.
如图所示,△ABC的顶点与点O在8×8的网格中的格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com