
【题目】如图,在平面直角坐标系xOy中,菱形AOBC的一个顶点O在坐标原点,一边OB在x轴的正半轴上,sin∠AOB=![]() ,反比例函数y=
,反比例函数y=![]() 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
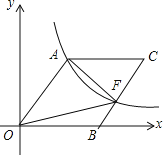
A. 30B. 40C. 60D. 80
【答案】B
【解析】
过点A作AM⊥x轴于点M,设OA=a,通过解直角三角形找出点A的坐标,结合反比例函数图象上点的坐标特征即可求出a的值,再根据四边形OACB是菱形、点F在边BC上,即可得出S△AOF=![]() S菱形OBCA,结合菱形的面积公式即可得出结论.
S菱形OBCA,结合菱形的面积公式即可得出结论.
过点A作AM⊥x轴于点M,如图所示.
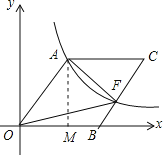
设OA=a,
在Rt△OAM中,∠AMO=90°,OA=a,sin∠AOB=![]() ,
,
∴AM=OAsin∠AOB=![]() a,OM=
a,OM=![]() =
=![]() a,
a,
∴点A的坐标为(![]() a,
a,![]() a).
a).
∵点A在反比例函数y=![]() 的图象上,
的图象上,
∴![]() a
a![]() a=
a=![]() a2=48,
a2=48,
解得:a=10,或a=-10(舍去).
∴AM=8,OM=6,OB=OA=10.
∵四边形OACB是菱形,点F在边BC上,
∴S△AOF=![]() S菱形OBCA=
S菱形OBCA=![]() OBAM=40.
OBAM=40.
故选:B.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
(1)求反比例函数的表达式;
(2)将直线l1:y=﹣![]() x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 的网格中,每个小正方形的边长均为
的网格中,每个小正方形的边长均为![]() ,线段
,线段![]() 的端点都在小正方形的顶点上.(要求:下面所画图形的点
的端点都在小正方形的顶点上.(要求:下面所画图形的点![]() 都在小正方形的顶点上)
都在小正方形的顶点上)
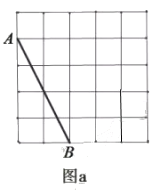
![]() 在图
在图![]() 中画一个以线段
中画一个以线段![]() 为一边的等腰三角形
为一边的等腰三角形![]() ,
,![]() ,使
,使![]() 的面积是
的面积是![]() .
.
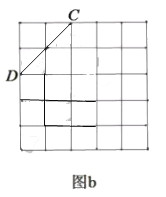
![]() 在图
在图![]() 中画一个以线段
中画一个以线段![]() 为一边的矩形
为一边的矩形![]() ,使矩形
,使矩形![]() 的面积是
的面积是![]() ,并直接写出矩形
,并直接写出矩形![]() 的周长
的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD是菱形,边BC在x轴上,点A(0,4),点B(3,0),双曲线y=![]() 与直线BD交于点D、点E.
与直线BD交于点D、点E.
(1)求k的值;
(2)求直线BD的解析式;
(3)求△CDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机抽取了本校部分学生进行问卷调查(必选且只选一类节目),将调查结果进行整理后,绘制了如下不完整的条形统计图和扇形统计图,其中喜爱体育节目的学生人数比喜爱戏曲节目的学生人数的3倍还多1人.
请根据所给信息解答下列问题:
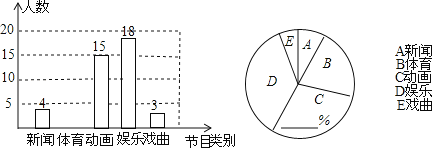
(1)求本次抽取的学生人数.
(2)补全条形图,在扇形统计图中的横线上填上正确的数值,并直接写出“体育”对应的扇形圆心角的度数.
(3)该校有3000名学生,求该校喜爱娱乐节目的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
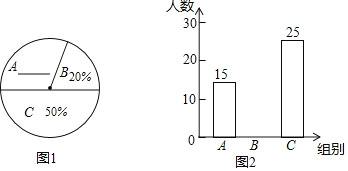
【题目】为响应国家“厉行节约,反对浪费”的号召,某班一课外活动小组成员在全校范围内随机抽取了若干名学生,针对“你每天是否会节约粮食”这个问题进行了调查,并将调查结果分成三组(A.会;B.不会;C.有时会),绘制了两幅不完整的统计图(如图)
(1)这次被抽查的学生共有______人,扇形统计图中,“A组”所对应的圆心度数为______;
(2)补全两个统计图;
(3)如果该校学生共有2000人,请估计“每天都会节约粮食”的学生人数;
(4)若不节约零食造成的浪费,按平均每人每天浪费5角钱计算,小江认为,该校学生一年(365天)共将浪费:2000×20%×0.5×365=73000(元),你认为这种说法正确吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济南某中学在参加“创文明城,点赞泉城”书画比赛中,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作鼎的数量进行了分析统计,制作了两幅不完整的统计图.

请根据以上信息,回答下列问题:
(l)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
(2)请补充完整条形统计图,并计算扇形统计图中C班作品数量所对应的圆心角度数 .
(3)请估计全校共征集作品的什数.
(4)如果全枝征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一样等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1x2|≥|y1y2|,则点P1与点P2的“非常距离”为|x1x2|;
若|x1x2||y1y2|,则点P1与点P2的“非常距离”为|y1y2|.
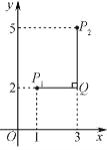
例如:点P1(1,2),点P2(3,5),因为|13||25|,所以点P1与点P2的“非常距离”为|25|3,也就是图中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).
(1)已知点A(0,1),
①在B(![]() ,0),C(2,1),D(1,2),E(0,
,0),C(2,1),D(1,2),E(0,![]() )四个点中,与点A的“非常距离”为
)四个点中,与点A的“非常距离”为![]() 的点是;
的点是;
②点F为x轴上一动点,直接写出点A与点F的“非常距离”的最小值;
(2)已知点M是直线y2x6上的一个动点,
①点G的坐标是(0,2),求点M与点G的“非常距离”的最小值及相应的点M的坐标;
①点N是以点(4,0)为圆心,![]() 为半径的圆上的一个动点,直接写出点M与点N的“非常距离”的最小值及相应的点M的坐标.
为半径的圆上的一个动点,直接写出点M与点N的“非常距离”的最小值及相应的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-4x+3.
(1)用配方法求其图象的顶点C的坐标,并描述该函数的函数值随自变量的增减而变化的情况;
(2)求函数图象与x轴的交点A,B的坐标,及△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com