
(10分)(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC= ,其中
,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状,并给出证明.

见解析
【解析】
试题分析:1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA,则AE=BD,AD=CE,于是DE=AE+AD=BD+CE;(2)与(1)的证明方法一样;(3)与前面的结论得到△ADB≌△CEA,则BD=AE,∠DBA=∠CAE,根据等边三角形的性质得∠ABF=∠CAF=60°,则∠DBA+∠ABF=∠CAE+∠CAF,则∠DBF=∠FAE,利用“SAS”可判断△DBF≌△EAF,所以DF=EF,∠BFD=∠AFE,于是∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,根据等边三角形的判定方法可得到△DEF为等边三角形.
试题解析:证明:(1)∵BD⊥直线m,CE⊥直线m

∴∠BDA=∠CEA=90°
∵∠BAC=90°
∴∠BAD+∠CAE=90°
∵∠BAD+∠ABD=90°
∴∠CAE=∠ABD 1分
又AB=AC
∴△ADB≌△CEA 2分
∴AE=BD,AD=CE
∴DE=AE+AD= BD+CE 3分
(2)∵∠BDA =∠BAC=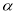 ,
,

∴∠DBA+∠BAD=∠BAD +∠CAE=180°—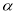
∴∠DBA=∠CAE 4分
∵∠BDA=∠AEC=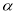 ,AB=AC
,AB=AC
∴△ADB≌△CEA 5分
∴AE=BD,AD=CE
∴DE=AE+AD=BD+CE 6分
(3)由(2)知,△ADB≌△CEA,
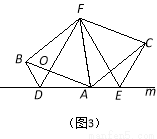
BD=AE,∠DBA =∠CAE
∵△ABF和△ACF均为等边三角形
∴∠ABF=∠CAF=60°]
∴∠DBA+∠ABF=∠CAE+∠CAF
∴∠DBF=∠FAE 8分
∵BF=AF
∴△DBF≌△EAF 9分
∴DF=EF,∠BFD=∠AFE
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°
∴△DEF为等边三角形. 10分
考点:1.全等三角形的判定与性质; 2.等边三角形的判定.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年浙江省余姚市八年级上学期期中考试数学试卷(解析版) 题型:解答题
(本小题满分8分)如图,已知AE∥BC,AE平分∠DAC.求证:AB=AC.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省嘉兴市实验学校九年级上学期期中考试数学试卷(解析版) 题型:填空题
“服务社会,提升自我.”一中实验学校积极开展志愿者服务活动,来自九年级的5名同学(三男两女)成立了“交通秩序维护”小分队.若从该小分队任选两名同学进行交通秩序维护,则恰是一男一女的概率是
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省嘉兴市八年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:
①△AED≌△AEF
②△AED为等腰三角形
③BE+DC>DE
④BE2+DC2=DE2 ,
其中正确结论的个数是( )

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省嘉兴市八年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,在△ABC中,DE是AC的中垂线,AD=5,BD=2,则BC的长是 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省嘉兴市实验初学七年级上学期期中考试数学试卷(解析版) 题型:选择题
4个有理数相乘,积的符号是负号,则这4个有理数中,负数有( )
A.1个或3个 B.1个或2个 C.2个或4个 D.3个或4个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省嘉兴市实验初学七年级上学期期中考试数学试卷(解析版) 题型:填空题
在数轴原点右侧,且与表示-1的点距离2个单位长度的点所表示的数是_______。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省嘉兴市实验初学七年级上学期期中考试数学试卷(解析版) 题型:解答题
(8分)小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图。根据图中的数据(单位:m),解答下列问题:

(1)用含 、
、 的代数式表示地面总面积;
的代数式表示地面总面积;
(2)已知铺1m2地砖的平均费用为180元,当 =5,
=5, =1时,求铺这套经济房所需地砖的总费用为多少元?
=1时,求铺这套经济房所需地砖的总费用为多少元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省宁波市九年级10月月考数学试卷(解析版) 题型:解答题
(本题满分12分)某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中 .准备在形如Rt
.准备在形如Rt 的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形
的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形 内种植紫色花草,每种花草的价格如下表:
内种植紫色花草,每种花草的价格如下表:
品种 | 红色花草 | 黄色花草 | 紫色花草 |
价格(元/米2) | 60 | 80 | 120 |
设 的长为
的长为 米,正方形
米,正方形 的面积为
的面积为 平方米,买花草所需的费用为
平方米,买花草所需的费用为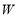 元,解答下列问题:
元,解答下列问题:
(1) 与
与 之间的函数关系式为
之间的函数关系式为 ;
;
(2)求 与
与 之间的函数关系式,并求所需的最低费用是多少元;
之间的函数关系式,并求所需的最低费用是多少元;
(3)当买花草所需的费用最低时,求 的长.
的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com