
【题目】如图1,ABCD为正方形,直线MN分别过AD边与BC边的中点,点P为直线MN上任意一点,连接PB、PC分别与AD边交于E、F两点,PC与BD交于点K,连接AK与PB交于点G.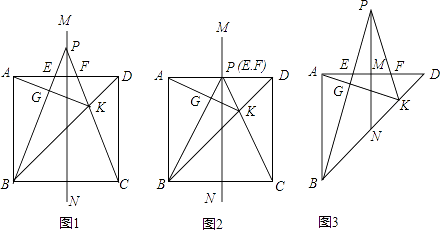
(1)探索发现
当点P落在AD边上时,如图2,试探究PB与AK的位置关系以及PB、PK、AK三者的数量关系(直接写出无需证明);
(2)延伸拓展
当点P落在正方形外,如图1,以上两个结论是否仍然成立?如果成立请给出证明,如果不成立请说明你的理由;
(3)应用推广
如图3,在等腰Rt△ABD中,其中∠BAD=90°,腰长为3,M、N分别为AD边与BD边的中点,K为线段DN中点,F为AD边上靠近于D的三等分点.连接KF并延长与直线MN交于点P,连接PB分别与AD、AK交于点E、G.试求四边形EFKG的周长及面积.
【答案】
(1)
解:PB⊥AK,PB=PK+AK;
理由:如图2中,
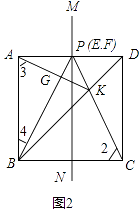
∵点P在MN上,根据对称性易得∠PBC=∠2且PB=PC,
又∠ABK=∠CBK=45°,
在△BKA和△BKC中,
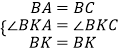
∴△ABK≌△CBK,
∴∠2=∠3且AK=CK,
∴∠PBC=∠3.
又∠PBC+∠4=90°,
∴∠3+∠4=90°,
即PB⊥AK.
∴PB=PC=PK+CK=PK+AK.
(2)
以上两个结论仍然成立,
理由如下:如图1中,

∵点P在MN上,根据对称性易得∠PBC=∠2且PB=PC,
又∠ABK=∠CBK=45°,
在△BKA和△BKC中,
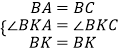
∴△ABK≌△CBK,
∴∠2=∠3且AK=CK,
∴∠PBC=∠3.
又∠PBC+∠4=90°,
∴∠3+∠4=90°,
即PB⊥AK.
∴PB=PC=PK+CK=PK+AK.
(3)
如图3中,过点B作AD的平行线交PK延长线与点C,连接CD.
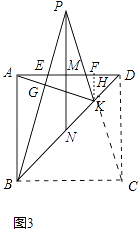
∵FD∥BD,
∴△FDK∽△CBK.
又DK:BK=1:3,
∴FD:BC=1:3.
∵FD:AD=1:3,
∴BC=AD.
∵BC∥AD且AB⊥AD且AB=AD,
∴四边形ABCD为正方形.
∵PB=PK+AK,
即(PE+BE)=(PF+FK)+AK,又PE=PF,
∴BE=FK+AK.
在Rt△EAB中,∵AE=1,AB=3,
∴BE= ![]() =
= ![]() .
.
∵AG⊥BE(上一问结论),
∵Rt△AGE∽Rt△BGA,且相似比为1:3,
设EG=t,AG=3t,BG=9t,
∴BE=10t= ![]() ,
,
∴ ![]() .
.
∴四边形EFKG的周长=EF+FK+GK+EG=EF+(FK+AK)﹣AG+EG
=EF+BE﹣AG+EG=1+10t﹣3t+t=1+8t= ![]() .
.
过点K作AD垂线,垂足为H,
∵HK∥AB且DK:DB=1:4,
∴KH= ![]() AB=
AB= ![]() ,
,
∴S四边形EFGH=S△AFK﹣S△AEG= ![]() AFKH﹣
AFKH﹣ ![]() AGEG=
AGEG= ![]() 2
2 ![]() ﹣
﹣ ![]() 3tt=
3tt= ![]() .
.
【解析】●探索发现 PB⊥AK,PB=PK+AK,只要证明∠3=∠4=90°即可证明PB⊥AK,由△ABK≌△CBK,结合PB=PC即可解决问题.
●延伸拓展 以上两个结论仍然成立,证明方法类似上面.
●应用推广 如图3中,过点B作AD的平行线交PK延长线与点C,连接CD,利用上面结论结合条件即可解决问题.
【考点精析】解答此题的关键在于理解相似三角形的应用的相关知识,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+2x经过原点O,且与直线y=x﹣2交于B,C两点.
(1)求抛物线的顶点A的坐标及点B,C的坐标;
(2)求证:∠ABC=90°;
(3)在直线BC上方的抛物线上是否存在点P,使△PBC的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(4)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店打出促销广告:最潮新款服装50件,每件售价300元,若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低2元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题: 
(1)一共调查了多少名学生;
(2)请补全条形统计图;
(3)若该校共有6000名学生,根据以上调查结果估计该校全体学生每天参与户外活动所用的总时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题: 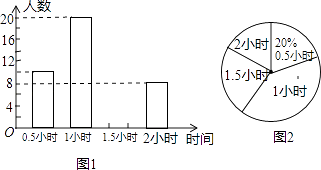
(1)一共调查了多少名学生;
(2)请补全条形统计图;
(3)若该校共有6000名学生,根据以上调查结果估计该校全体学生每天参与户外活动所用的总时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,8),点P在边BC上以每秒1个单位长的速度由点C向点B运动,同时点Q在边AB上以每秒a个单位长的速度由点A向点B运动,运动时间为t秒(t>0).
(1)若反比例函数y= ![]() 图象经过P点、Q点,求a的值;
图象经过P点、Q点,求a的值;
(2)若OQ垂直平分AP,求a的值;
(3)当Q点运动到AB中点时,是否存在a使△OPQ为直角三角形?若存在,求出a的值,若不存在请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展以感恩教育为主题的艺术活动,举办了四个项目的比赛,它们分别是演讲、唱歌、书法、绘画.要求每位同学必须参加,且限报一项活动.以九年级(1)班为样本进行统计,并将统计结果绘成如图1、图2所示的两幅统计图.请你结合图示所给出的信息解答下列问题. 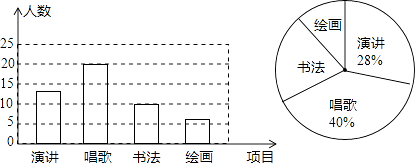
(1)求出参加绘画比赛的学生人数占全班总人数的百分比?
(2)求出扇形统计图中参加书法比赛的学生所在扇形圆心角的度数?
(3)若该校九年级学生有600人,请你估计这次艺术活动中,参加演讲和唱歌的学生各有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com