
【题目】问题提出
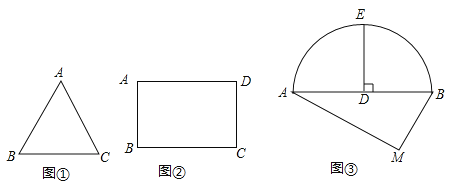
(1)如图①,△ABC是等边三角形,AB=12,若点O是△ABC的内心,则OA的长为 ;
问题探究
(2)如图②,在矩形ABCD中,AB=12,AD=18,如果点P是AD边上一点,且AP=3,那么BC边上是否存在一点Q,使得线段PQ将矩形ABCD的面积平分?若存在,求出PQ的长;若不存在,请说明理由.
问题解决
(3)某城市街角有一草坪,草坪是由△ABM草地和弦AB与其所对的劣弧围成的草地组成,如图③所示.管理员王师傅在M处的水管上安装了一喷灌龙头,以后,他想只用喷灌龙头来给这块草坪浇水,并且在用喷灌龙头浇水时,既要能确保草坪的每个角落都能浇上水,又能节约用水,于是,他让喷灌龙头的转角正好等于∠AMB(即每次喷灌时喷灌龙头由MA转到MB,然后再转回,这样往复喷灌.)同时,再合理设计好喷灌龙头喷水的射程就可以了.
如图③,已测出AB=24m,MB=10m,△AMB的面积为96m2;过弦AB的中点D作DE⊥AB交![]() 于点E,又测得DE=8m.
于点E,又测得DE=8m.
请你根据以上信息,帮助王师傅计算喷灌龙头的射程至少多少米时,才能实现他的想法?为什么?(结果保留根号或精确到0.01米)
【答案】(1)![]() ;(2)PQ=
;(2)PQ=![]() ;(3)喷灌龙头的射程至少为19.71米.
;(3)喷灌龙头的射程至少为19.71米.
【解析】
试题分析:(1)构建Rt△AOD中,利用cos∠OAD=cos30°=![]() ,可得OA的长;
,可得OA的长;
(2)经过矩形对角线交点的直线将矩形面积平分,根据此结论作出PQ,利用勾股定理进行计算即可;
(3)如图3,作辅助线,先确定圆心和半径,根据勾股定理计算半径:
在Rt△AOD中,由勾股定理解得:r=13根据三角形面积计算高MN的长,证明△ADC∽△ANM,列比例式求DC的长,确定点O在△AMB内部,利用勾股定理计算OM,则最大距离FM的长可利用相加得出结论.
试题解析:(1)如图1,过O作OD⊥AC于D,则AD=![]() AC=
AC=![]() ×12=6,∵O是内心,△ABC是等边三角形,∴∠OAD=
×12=6,∵O是内心,△ABC是等边三角形,∴∠OAD=![]() ∠BAC=
∠BAC=![]() ×60°=30°,在Rt△AOD中,cos∠OAD=cos30°=
×60°=30°,在Rt△AOD中,cos∠OAD=cos30°=![]() ,∴OA=6÷
,∴OA=6÷![]() =
=![]() ,故答案为:
,故答案为:![]() ;
;
(2)存在,如图2,连接AC、BD交于点O,连接PO并延长交BC于Q,则线段PQ将矩形ABCD的面积平分,∵点O为矩形ABCD的对称中心,∴CQ=AP=3,过P作PM⊥BC于点,则PM=AB=12,MQ=18﹣3﹣3=12,由勾股定理得:PQ=![]() =
=![]() =
=![]() ;
;
(3)如图3,作射线ED交AM于点C.∵AD=DB,ED⊥AB,![]() 是劣弧,∴
是劣弧,∴![]() 所在圆的圆心在射线DC上,假设圆心为O,半径为r,连接OA,则OA=r,OD=r﹣8,AD=
所在圆的圆心在射线DC上,假设圆心为O,半径为r,连接OA,则OA=r,OD=r﹣8,AD=![]() AB=12,在Rt△AOD中,r2=122+(r﹣8)2,解得:r=13,∴OD=5,过点M作MN⊥AB,垂足为N,∵S△ABM=96,AB=24,∴
AB=12,在Rt△AOD中,r2=122+(r﹣8)2,解得:r=13,∴OD=5,过点M作MN⊥AB,垂足为N,∵S△ABM=96,AB=24,∴![]() ABMN=96,
ABMN=96,![]() ×24×MN=96,∴MN=8,NB=6,AN=18,∵CD∥MN,∴△ADC∽△ANM,∴
×24×MN=96,∴MN=8,NB=6,AN=18,∵CD∥MN,∴△ADC∽△ANM,∴![]() ,∴
,∴![]() ,
,![]() ,∴OD<CD,∴点O在△AMB内部,∴连接MO并延长交
,∴OD<CD,∴点O在△AMB内部,∴连接MO并延长交![]() 于点F,则MF为草坪上的点到M点的最大距离,∵在
于点F,则MF为草坪上的点到M点的最大距离,∵在![]() 上任取一点异于点F的点G,连接GO,GM,∴MF=OM+OF=OM+OG>MG,即MF>MG,过O作OH⊥MN,垂足为H,则OH=DN=6,MH=3,∴OM=
上任取一点异于点F的点G,连接GO,GM,∴MF=OM+OF=OM+OG>MG,即MF>MG,过O作OH⊥MN,垂足为H,则OH=DN=6,MH=3,∴OM=![]() =
=![]() =
=![]() ,∴MF=OM+r=
,∴MF=OM+r=![]() +13≈19.71(米).
+13≈19.71(米).
答:喷灌龙头的射程至少为19.71米.



 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】探索函数y=x+ ![]() 的图象和性质:
的图象和性质:
(1)它的自变量取值范围是;
(2)当x>0时,我们利用列表法画出函数图象
①填写下表,画出函数的图象:
x | … |
|
|
| 1 | 2 | 3 | 4 | … |
y | … | … |

②观察图象,我们发现函数图象有一个最低点,它的坐标是 ![]() ,这说明当x=
,这说明当x= ![]() ,函数y有最小值是
,函数y有最小值是 ![]() ;并且,在该点的左边,y随x的增大而
;并且,在该点的左边,y随x的增大而 ![]() ,在该点的右边,y随x的增大而
,在该点的右边,y随x的增大而 ![]() .
.
③利用上述结论,解决问题:矩形ABCD的面积等于1,当它的长和宽分别为多少时,它的周长最小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , …,按照此规律继续下去,则S2017的值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在精准扶贫中,某村的李师傅在县政府的扶持下,去年下半年,他对家里的3个温室大棚进行修整改造,然后,1个大棚种植香瓜,另外2个大棚种植甜瓜,今年上半年喜获丰收,现在他家的甜瓜和香瓜已全部售完,他高兴地说:“我的日子终于好了”.
最近,李师傅在扶贫工作者的指导下,计划在农业合作社承包5个大棚,以后就用8个大棚继续种植香瓜和甜瓜,他根据种植经验及今年上半年的市场情况,打算下半年种植时,两个品种同时种,一个大棚只种一个品种的瓜,并预测明年两种瓜的产量、销售价格及成本如下:
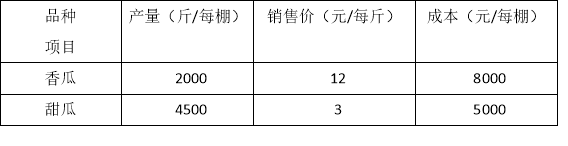
现假设李师傅今年下半年香瓜种植的大棚数为x个,明年上半年8个大棚中所产的瓜全部售完后,获得的利润为y元.
根据以上提供的信息,请你解答下列问题:
(1)求出y与x之间的函数关系式;
(2)求出李师傅种植的8个大棚中,香瓜至少种植几个大棚?才能使获得的利润不低于10万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,AB=BC,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3 . 若l1与l2的距离为4,l2与l3的距离为6,则Rt△ABC的面积为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com