
【题目】如图,Rt△ABC中,∠ABC=90°,AB=BC,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3 . 若l1与l2的距离为4,l2与l3的距离为6,则Rt△ABC的面积为 . 
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】问题提出
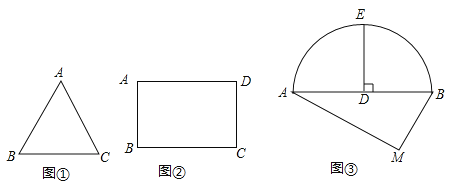
(1)如图①,△ABC是等边三角形,AB=12,若点O是△ABC的内心,则OA的长为 ;
问题探究
(2)如图②,在矩形ABCD中,AB=12,AD=18,如果点P是AD边上一点,且AP=3,那么BC边上是否存在一点Q,使得线段PQ将矩形ABCD的面积平分?若存在,求出PQ的长;若不存在,请说明理由.
问题解决
(3)某城市街角有一草坪,草坪是由△ABM草地和弦AB与其所对的劣弧围成的草地组成,如图③所示.管理员王师傅在M处的水管上安装了一喷灌龙头,以后,他想只用喷灌龙头来给这块草坪浇水,并且在用喷灌龙头浇水时,既要能确保草坪的每个角落都能浇上水,又能节约用水,于是,他让喷灌龙头的转角正好等于∠AMB(即每次喷灌时喷灌龙头由MA转到MB,然后再转回,这样往复喷灌.)同时,再合理设计好喷灌龙头喷水的射程就可以了.
如图③,已测出AB=24m,MB=10m,△AMB的面积为96m2;过弦AB的中点D作DE⊥AB交![]() 于点E,又测得DE=8m.
于点E,又测得DE=8m.
请你根据以上信息,帮助王师傅计算喷灌龙头的射程至少多少米时,才能实现他的想法?为什么?(结果保留根号或精确到0.01米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A坐标为(2,0),以OA为边在第一象限内作等边△OAB,点C为x轴上一动点,且在点A右侧,连接BC,以BC为边在第一象限内作等边△BCD,连接AD交BC于E.
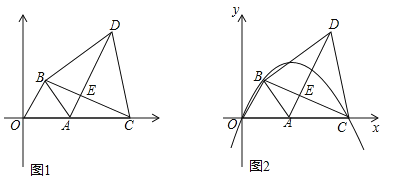
(1)①直接回答:△OBC与△ABD全等吗?
②试说明:无论点C如何移动,AD始终与OB平行;
(2)当点C运动到使AC2=AEAD时,如图2,经过O、B、C三点的抛物线为y1.试问:y1上是否存在动点P,使△BEP为直角三角形且BE为直角边?若存在,求出点P坐标;若不存在,说明理由;
(3)在(2)的条件下,将y1沿x轴翻折得y2,设y1与y2组成的图形为M,函数![]() 的图象l与M有公共点.试写出:l与M的公共点为3个时,m的取值.
的图象l与M有公共点.试写出:l与M的公共点为3个时,m的取值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABO中,A,B两点的坐标分别为(2,4),(7,2),C,G,F,E分别为过A,B两点所作的y轴、x轴的垂线与y轴、x轴的交点.求△AOB的面积.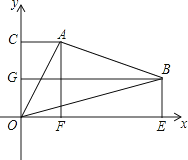
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB.CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
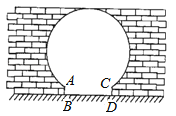
A.2米 B.2.5米 C.2.4米 D.2.1米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com