
【题目】如图1,在锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,且BF=AC。求证:ED平分∠FEC。
【答案】证明:∵AD⊥BC,BE⊥AC,∴∠BDF=∠ADC=90°,∠AEB=∠FEC=90°,
∵∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
在△BDF和△ADC中,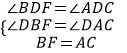
∴△BDF≌△ADC(AAS),
∴BD=AD,
∴∠BAD=∠ABD=45°,
∵∠AEB=∠ADB=90°,
∴A、B、D、E四点共圆,
∴∠BED=∠BAD=45°,
∴∠CED=90°-45°=45°=∠BED,
∴ED平分∠FEC.
【解析】由角的和差得到∠DBF=∠DAC,根据全等三角形的判定方法AAS,得到△BDF≌△ADC,得到对应边相等,由四点共圆和圆周角定理,得到ED平分∠FEC.


科目:初中数学 来源: 题型:
【题目】在频数分布直方图中,有11个小长方形,若中间一个小长方形的面积等于其它10个小长方形面积的和的 ![]() ,且数据有160个,则中间一组的频数为( )
,且数据有160个,则中间一组的频数为( )
A.32
B.0.2
C.40
D.0.25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠E=∠F,∠B=∠C,AE=AF,以下结论:①∠FAN=∠EAM;②EM=FN;③△ACN≌△ABM;④CD=DN.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(0,0),B(2,﹣2),C(4,0),D(2,2),则以这四个点为顶点的四边形ABCD是( )
A. 正方形 B. 菱形 C. 梯形 D. 矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,对称轴为直线x=![]() 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A.
的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A.
(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com