
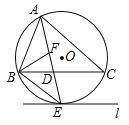
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
【答案】(1)直线l与⊙O相切;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)连接OE、OB、OC.由题意可证明![]() ,于是得到∠BOE=∠COE,由等腰三角形三线合一的性质可证明OE⊥BC,于是可证明OE⊥l,故此可证明直线l与⊙O相切;
,于是得到∠BOE=∠COE,由等腰三角形三线合一的性质可证明OE⊥BC,于是可证明OE⊥l,故此可证明直线l与⊙O相切;
(2)先由角平分线的定义可知∠ABF=∠CBF,然后再证明∠CBE=∠BAF,于是可得到∠EBF=∠EFB,最后依据等角对等边证明BE=EF即可;
(3)先求得BE的长,然后证明△BED∽△AEB,由相似三角形的性质可求得AE的长,于是可得到AF的长.
试题解析:(1)直线l与⊙O相切.
理由:如图1所示:连接OE、OB、OC.
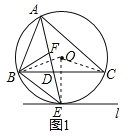
∵AE平分∠BAC,∴∠BAE=∠CAE,∴![]() ,∴∠BOE=∠COE.
,∴∠BOE=∠COE.
又∵OB=OC,∴OE⊥BC.
∵l∥BC,∴OE⊥l,∴直线l与⊙O相切.
(2)∵BF平分∠ABC,∴∠ABF=∠CBF.
又∵∠CBE=∠CAE=∠BAE,∴∠CBE+∠CBF=∠BAE+∠ABF.
又∵∠EFB=∠BAE+∠ABF,∴∠EBF=∠EFB,∴BE=EF.
(3)由(2)得BE=EF=DE+DF=7.∵∠DBE=∠BAE,∠DEB=∠BEA,∴△BED∽△AEB,∴![]() ,即
,即![]() ,解得;AE=
,解得;AE=![]() ,∴AF=AE﹣EF=
,∴AF=AE﹣EF=![]() ﹣7=
﹣7=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】2015年初,一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快车从“中国制造”到“中国创造”的飞跃,将300000用科学记数法表示为( )
A.3×106
B.3×105
C.0.3×106
D.30×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店新开张,第一天销售服装a件,第二天比第一天少销售14件,第三天的销售量是第二天的2倍多10件,则这三天销售了( )件.
A. 3a﹣42 B. 3a+42 C. 4a﹣32 D. 3a+32
查看答案和解析>>
科目:初中数学 来源: 题型:
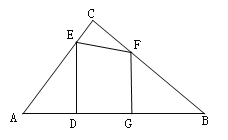
【题目】如图,在Rt△ABC中,∠ACB=90,AB=10,AC=6,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
(1)当AD=3时,求DE的长;
(2)当点E、F在边AC、BC上移动时,设![]() ,
,![]() ,
,
求![]() 关于
关于![]() 的函数解析式。
的函数解析式。
(3)在点E、F移动过程中,△AED与△CEF能否相似,若能,求AD的长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标是(2,1),将点A绕原点O旋转180°得到点A′,则点A′的坐标是( )
A.(-1,-2)B.(1,-2)C.(-2,-1)D.(2,-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,CE⊥AD于E,BF∥AC交CE的延长线于F.
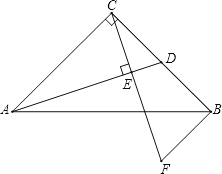
(1)求证:△ACD≌△CBF;
(2)求证:AB垂直平分DF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com