
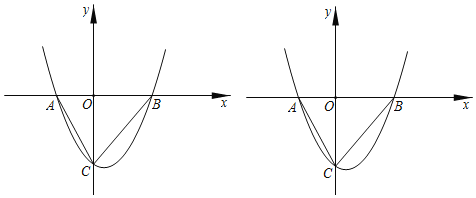
【题目】已知抛物线y=ax2+bx+c经过点A,点B,与y轴负半轴交于点C,且OC=OB,其中B点坐标为(3,0),对称轴为直线x=![]() .
.
(1)求抛物线的解析式;
(2)在x轴上方有一点P(m,n),连接PA后满足∠PAB=∠CAB,记△PBC面积为S,求S与m的函数关系;
(3)在(2)的条件下,当点P恰好落在抛物上时,将直线BC上下平移,平移后的直线y=x+t与抛物线交于C',B'两点(C'在B'的左侧),若以点C'、B'、P为顶点三角形是直角三角形,求t的值.
【答案】(1)![]() ;(2)S=
;(2)S=![]() m+9(m>﹣2);(3)t的值为19或32.
m+9(m>﹣2);(3)t的值为19或32.
【解析】
(1)先确定出点A坐标,再用待定系数法即可得出结论;
(2)先确定出直线AP的解析式,进而用m表示点P的坐标,即可得出结论;
(3)先确定出点P的坐标,当∠B'PC'=90°时,利用根与系数的关系确定出B'C'的中点E的坐标,利用B'C'=2PE建立方程求解,当∠PC'B'=90°时,先确定出点G的坐标,进而求出直线C'G的解析式,进而得出点C'的坐标,即可得出结论.
(1)∵B(3,0),对称轴为直线x=![]() ,
,
∴A(﹣2,0),
∴设抛物线的解析式为y=a(x+2)(x﹣3)=ax2﹣ax﹣6a,
∵B(3,0),
∴OB=3,
∵OC=OB,
∴OC=3,
∴C(0,﹣3),
把C(0,﹣3)代入y=a(x+2)(x﹣3),
∴﹣6a=﹣3,
∴a=![]() ,
,
∴抛物线的解析式为![]() ;
;
(2)如图1,射线AP与y轴的交点记作点C',
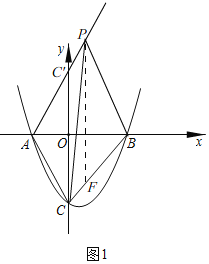
∵∠BAC=∠BAC',OA=OA,∠AOC=∠AOC'=90°,
∴△AOC≌△AOC'(ASA),
∴OC'=OC=3,
∴C'(0,3),
∵A(﹣2,0),
设直线AP的解析式为![]() ,
,
∵![]() ,
,
解得:![]() ,
,
∴直线AP的解析式为y=![]() x+3,
x+3,
∵点P(m,n)在直线AP上,
∴n=![]() m+3,
m+3,
∵B(3,0),C(0,﹣3),
直线BC的解析式为![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴直线BC的解析式为y=x﹣3,
过点P作y轴的平行线交BC于F,
∴F(m,m﹣3),
∴PF=![]() m+3﹣(m﹣3)=
m+3﹣(m﹣3)=![]() m+6,
m+6,
∴S=S△PBC=![]() OBPF=
OBPF=![]() ×3(
×3(![]() m+6)=
m+6)=![]() m+9(m>﹣2);
m+9(m>﹣2);
(3)由(1)知,抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣3①
x﹣3①
由(2)知,直线AP的解析式为y=![]() x+3②,
x+3②,
联立①②解得,![]() 或
或![]() ,
,
∴P(6,12),
如图2,
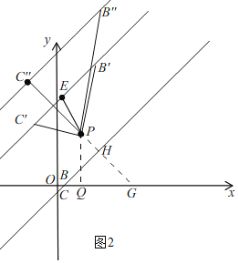
当∠C'PB'=90°时,取B'C'的中点E,连接PE,
则B'C'=2PE,即:B'C'2=4PE2,
设B'(x1,y1),C'(x2,y2),
∵直线B'C'的解析式为y=x+t③,
联立①③化简得,x2﹣3x﹣(2t+6)=0,
∴x1+x2=3,x1x2=﹣(2t+6),
∴点E(![]() ,
,![]() +t),
+t),
B'C'2=(x1﹣x2)2+(y1﹣y2)2=2(x1﹣x2)2=2[(x1+x2)2﹣4x1x2]
=2[9+4(2t+6)]=16t+66,
而PE2=(6﹣![]() )2+(12﹣
)2+(12﹣![]() ﹣t)2=t2﹣21t+
﹣t)2=t2﹣21t+![]() ,
,
∴16t+66=4(t2﹣21t+![]() ),
),
∴t=6(此时,恰好过点P,舍去)或t=19,
当∠P![]() =90°时,延长
=90°时,延长![]() P交BC于H,交x轴于G,
P交BC于H,交x轴于G,
则∠BHG=90°,
∵OB=CO,∠BOC=90°,
∴∠OBC=45°,
∴∠PGO=45°,
过点P作PQ⊥x轴于Q,则GQ=PQ=12,
∴OG=OQ+GQ=18,
∴点G(18,0),
∴直线C'G的解析式为y=﹣x+18④,
联立①④解得![]() 或
或![]()
∴C'的坐标为(﹣7,25),
将点C'坐标代入y=x+t中,得25=﹣7+t,
∴t=32,
即:满足条件的t的值为19或32.


科目:初中数学 来源: 题型:
【题目】已知:如图点A,E,F,C在同一直线上,AE=EF=FC,过E,F分别作DE⊥AC,BF⊥AC,连结AB,CD,BD,BD交AC于点G,若AB=CD.
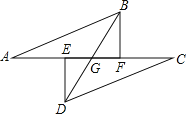
(1)求证:△ABF≌△CDE.
(2)若AE=ED=2,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两只捕捞船同时从A港出海捕鱼.甲船以每小时![]() 千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进.甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.
千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进.甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.
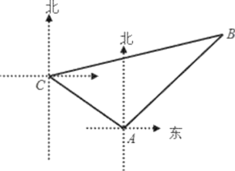
(1)甲船从C处追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是每小时多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数.将骰子抛掷两次,掷第一次,将朝上一面的点数记为![]() ,掷第二次,将朝上一面的点数记为
,掷第二次,将朝上一面的点数记为![]() ,则点(
,则点(![]() )落在直线
)落在直线![]() 上的概率为:
上的概率为:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(1,0),B(4,0),M(5,3).动点P从点A出发,沿x轴以每秒1个单位长的速度向右移动,且过点P的直线l:y=-x+b也随之移动.设移动时间为t秒.
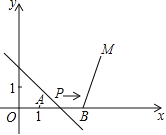
(1)当t=1时,求l的解析式;
(2)若l与线段BM有公共点,确定t的取值范围;
(3)直接写出t为何值时,点M关于l的对称点落在y轴上.如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD和矩形ABEF中,AC与DF相交于点G.
(1) 试说明DF=CE;
(2) 若AC=BF=DF,求∠ACE的度数.
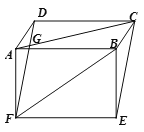
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知△ABC内接于⊙O,BC交直径AD于点E,过点C作AD的垂线交AB的延长线于点G,垂足为F,连接OC.
(1)求证:∠ACB=∠G;
(2)如图②,连接OB,若AB=AE,![]() ,求
,求![]() 的值.
的值.
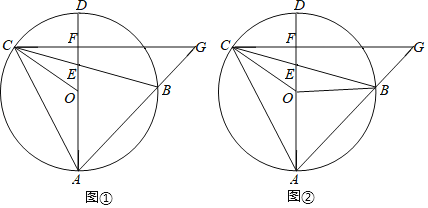
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com