
【题目】如图,甲、乙两只捕捞船同时从A港出海捕鱼.甲船以每小时![]() 千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进.甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.
千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进.甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.
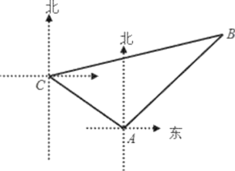
(1)甲船从C处追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是每小时多少千米?
【答案】(1)2小时;(2)甲船追赶乙船的速度是每小时15+15![]() 千米
千米
【解析】
(1)根据方向角可以得到∠BCA=45°,∠B=30度,过A作AD⊥BC于点D,在直角△ACD中,根据三角函数就可求得AD的长,再在直角△ABD中,根据三角函数即可求得AB的长,就可求得时间;
(2)求出BC的长,根据(1)中的结果求得时间,即可求得速度.
解:(1)如图,过A作AD⊥BC于点D.作CG∥AE交AD于点G.
∵乙船沿东北方向前进,
∴∠HAB=45°,
∵∠EAC=30°,
∴∠CAH=90°-30°=60°
∴∠CAB=60°+45°=105°.
∵CG∥EA,∴∠GCA=∠EAC=30°.
∵∠FCD=75°,∴∠BCG=15°,∠BCA=15°+30°=45°,
∴∠B=180°-∠BCA-∠CAB=30°.
在直角△ACD中,∠ACD=45°,AC=2×15![]() =30
=30![]() ,
,
AD=ACsin45°=3![]() ×
×![]() =30千米.
=30千米.
CD=ACcos45°=30千米.
在直角△ABD中,∠B=30°.
则AB=2AD=60千米.
则甲船从C处追赶上乙船的时间是:60÷15-2=2小时;
(2)BC=CD+BD=30+30![]() 千米.
千米.
则甲船追赶乙船的速度是每小时(30+30![]() )÷2=15+15
)÷2=15+15![]() 千米/小时.
千米/小时.
答:甲船从C处追赶上乙船用了2小时,甲船追赶乙船的速度是每小时15+15![]() 千米.
千米.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】为了帮助遭受自然灾害的地区,某学校号召同学们自愿捐款,已知第一次捐款总额为5800元,第二次捐款总额6000元,第二次捐款人数比第一次多20人,而且两次人均捐款额正好相等.
|
| |
每桶容积(升) | 20 | 15 |
每桶价格(元) | 5.6 | 4.5 |
(1)求两次各有多少人捐款?
(2)民政部门要求将捐款换成实物,统一运送到灾区.学校决定将捐款用于购买桶装水现有![]() 两种型号桶装水,上表是这两种桶装水的容积和单价.学校按民政局的救灾规划需订购总容积为40000升的桶装水,用同学们的捐款至少需订购
两种型号桶装水,上表是这两种桶装水的容积和单价.学校按民政局的救灾规划需订购总容积为40000升的桶装水,用同学们的捐款至少需订购![]() 型水多少桶.
型水多少桶.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且与双曲线
,且与双曲线![]() 的一个交点为
的一个交点为![]() ,将直线
,将直线![]() 在
在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折,得到一个“
轴翻折,得到一个“![]() ”形折线
”形折线![]() 的新函数.若点
的新函数.若点![]() 是线段
是线段![]() 上一动点(不包括端点),过点
上一动点(不包括端点),过点![]() 作
作![]() 轴的平行线,与新函数交于另一点
轴的平行线,与新函数交于另一点![]() ,与双曲线交于点
,与双曲线交于点![]() .
.
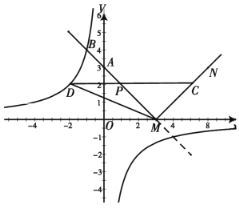
(1)若点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 的面积;(用含
的面积;(用含![]() 的式子表示)
的式子表示)
(2)探索:在点![]() 的运动过程中,四边形
的运动过程中,四边形![]() 能否为平行四边形?若能,求出此时点
能否为平行四边形?若能,求出此时点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
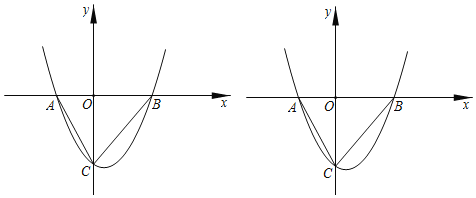
【题目】二次函数![]() 图象
图象![]() 轴上方的部分沿
轴上方的部分沿![]() 轴翻折到
轴翻折到![]() 轴下方,图象的其余部分保持不变,翻折后的图象与原图象
轴下方,图象的其余部分保持不变,翻折后的图象与原图象![]() 轴下方的部分组成一个“
轴下方的部分组成一个“![]() ”形状的新图象,若直线
”形状的新图象,若直线![]() 与该新图象有两个公共点,则
与该新图象有两个公共点,则![]() 的取值范围为_____.
的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠C=90°,点A、B在∠C的两边上,CA=30,CB=20,连结AB.点P从点B出发,以每秒4个单位长度的速度沿BC方向运动,到点C停止.当点P与B、C两点不重合时,作PD⊥BC交AB于D,作DE⊥AC于E.F为射线CB上一点,且∠CEF=∠ABC.设点P的运动时间为x(秒).
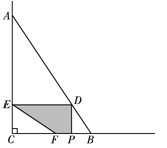
(1)用含有x的代数式表示CE的长;
(2)求点F与点B重合时x的值;
(3)当点F在线段CB上时,设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式;
(4)当x为某个值时,沿PD将以D、E、F、B为顶点的四边形剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合上述条件的x值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣![]() x+1与y轴交于点D.
x+1与y轴交于点D.

(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于
的图像交于![]() ,
,![]() 两点,与
两点,与![]() 轴分别交于
轴分别交于![]() 两点,且
两点,且![]() .
.
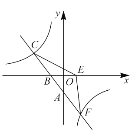
(1)求一次函数和反比例函数的解析式;
(2)若点![]() 与点
与点![]() 关于
关于![]() 轴对称,连接
轴对称,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c经过点A,点B,与y轴负半轴交于点C,且OC=OB,其中B点坐标为(3,0),对称轴为直线x=![]() .
.
(1)求抛物线的解析式;
(2)在x轴上方有一点P(m,n),连接PA后满足∠PAB=∠CAB,记△PBC面积为S,求S与m的函数关系;
(3)在(2)的条件下,当点P恰好落在抛物上时,将直线BC上下平移,平移后的直线y=x+t与抛物线交于C',B'两点(C'在B'的左侧),若以点C'、B'、P为顶点三角形是直角三角形,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人沿相同的路线由![]() 地到
地到![]() 地匀速前进,
地匀速前进,![]() 、
、![]() 两地之间的路程为20千米,他们距
两地之间的路程为20千米,他们距![]() 地的距离
地的距离![]() (单位:千米)与乙出发后的时间
(单位:千米)与乙出发后的时间![]() (单位:小时)的函数图象如图所示.根据图象信息,回答下列问题:
(单位:小时)的函数图象如图所示.根据图象信息,回答下列问题:

(1)甲的速度是 千米/小时,乙的速度是 千米/小时;
(2)是甲先出发还是乙先出发?先出发几小时?
(3)若乙到达![]() 地休息30分钟之后,立即以原来的速度返回
地休息30分钟之后,立即以原来的速度返回![]() 地,则在乙出发几小时以后两人再次相遇?
地,则在乙出发几小时以后两人再次相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com