练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

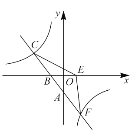
    【题目】如图，一次函数的图像与反比例函数的图像交于，两点，与轴分别交于两点，且．

    （1）求一次函数和反比例函数的解析式；

    （2）若点与点关于轴对称，连接，求的面积．

    【答案】（1）；（2）18.

    【解析】

    （1）先求出B点坐标，再用待定系数法求一次函数的解析式，再求出C点坐标，用待定系数法求反比例函数解析式；
    （2）先由对称性质求E点坐标，再联立方程组求得F点坐标，最后根据三角形面积公式求面积．

    解：（1）∵A（0，-3）
    ∴OA=3，
    ∵OA=OB，
    ∴OB=2，
    ∴B（-2，0）．

    将代入一次函数，得，解得

    一次函数的解析式为．

    点在一次函数的图像上，

    ．

    点在反比例函数的图像上，

    ，

    反比例函数的解析式为．

    （2）点与点关于轴对称，，

    ，

    ．

    联立解得或

    ，

    ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知二次函数的图象如图所示，对称轴为．下列结论中，正确的是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

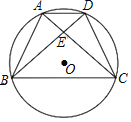
    【题目】如图，⊙O是四边形ABCD的外接圆，对角线AC与BD相交于点E，且AE＝DE，连接AD、CB．

    （1）求证：AB＝CD；

    （2）在不添加任何辅助线的情况下，直接写出图中所有的全等三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，甲、乙两只捕捞船同时从A港出海捕鱼．甲船以每小时千米的速度沿西偏北30°方向前进，乙船以每小时15千米的速度沿东北方向前进．甲船航行2小时到达C处，此时甲船发现渔具丢在乙船上，于是甲船快速（匀速）沿北偏东75°的方向追赶，结果两船在B处相遇．

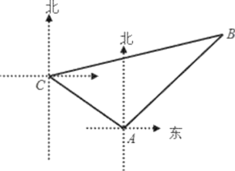
    （1）甲船从C处追赶上乙船用了多少时间？

    （2）甲船追赶乙船的速度是每小时多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

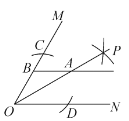
    【题目】如图，已知，以点为圆心，适当长度为半径作弧，分别交边于点，分别以为圆心，大于的长为半径作弧，两弧在内交于点，作射线．若是上一点，过点作的平行线交于点，且，则直线与之间的距离是（ ）

    A.B.C.3D.6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点为矩形的对角线上一动点，，，点为边的中点，则周长的最小值是_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数.将骰子抛掷两次，掷第一次，将朝上一面的点数记为，掷第二次，将朝上一面的点数记为，则点（）落在直线上的概率为：

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

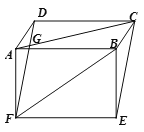
    【题目】已知：如图，在平行四边形ABCD和矩形ABEF中，AC与DF相交于点G.

    (1) 试说明DF＝CE；

    (2) 若AC＝BF＝DF，求∠ACE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

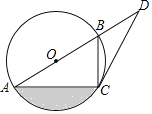
    【题目】如图，已知AB是⊙O上的点，C是⊙O上的点，点D在AB的延长线上，∠BCD=∠BAC．

    （1）求证：CD是⊙O的切线；

    （2）若∠D=30°，BD=2，求图中阴影部分的面积．

    查看答案和解析>>

    同步练习册答案