
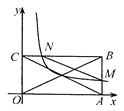
【题目】如图,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在平面直角坐标系的
分别在平面直角坐标系的![]() 轴和
轴和![]() 轴上,且
轴上,且![]() ,顶点
,顶点![]() 在第一象限,经过矩形
在第一象限,经过矩形![]() 对角线交点的反比例函数
对角线交点的反比例函数![]() 的图像分别与
的图像分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,若
,若![]() 的面积是2,则
的面积是2,则![]() 的值为________.
的值为________.
【答案】![]()
【解析】
设OC=a,则OA为2a,则B(2a,a),矩形的对角线交点为(a,![]() a),由点(a,
a),由点(a,![]() a)在反比例函数上,知a·
a)在反比例函数上,知a·![]() a=k,
a=k,![]() a2=k①;由M、N既在反比例函数上,又在矩形ABCD的边上,可设N(
a2=k①;由M、N既在反比例函数上,又在矩形ABCD的边上,可设N(![]() ,a),M(2a,
,a),M(2a,![]() ),可得BN=2a-
),可得BN=2a-![]() ,BM=a-
,BM=a-![]() ,由△NMB得面积为2,
,由△NMB得面积为2,
得![]() ·(2a-
·(2a-![]() )·(a-
)·(a-![]() )=2②,根据①②即可求出k的值
)=2②,根据①②即可求出k的值
设OC=a,则OA=2a,
故点B的坐标为(2a,a),矩形的对角线交点为(a,![]() a),
a),
∵反比例函数图像过(a,![]() a),
a),
∴a·![]() a=k,即a2=2k①,
a=k,即a2=2k①,
由M、N既在反比例函数上,又在矩形ABCD的边上,
可设N(![]() ,a),M(2a,
,a),M(2a,![]() ),
),
∴BN=2a-![]() ,BM=a-
,BM=a-![]() ,
,
∵△NMB得面积为2,
∴![]() ·(2a-
·(2a-![]() )·(a-
)·(a-![]() )=2 ②;
)=2 ②;
由①②解得k=![]() .
.


科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列所给的四个结论中,正确的是( )
(k≠0),下列所给的四个结论中,正确的是( )
A. 若点(2,4)在其图象上,则(﹣2,4)也在其图象上
B. 当k>0时,y随x的增大而减小
C. 过图象上任一点P作x轴、y轴的垂线,垂足分别A、B,则矩形OAPB的面积为k
D. 反比例函数的图象关于直线y=x和y=﹣x成轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC.
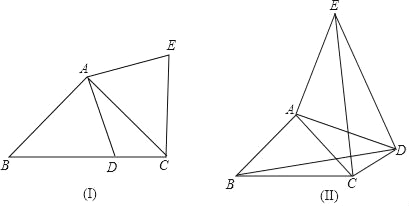
(I)如图,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC.
求证:(1)△BAD≌△CAE;
(2)BC=DC+EC.
(Ⅱ)如图,D为△ABC外一点,且∠ADC=45°,仍将线段AD绕点A逆时针旋转90°得到AE,连接EC,ED.
(1)△BAD≌△CAE的结论是否仍然成立?并请你说明理由;
(2)若BD=9,CD=3,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校教室A位于一地O的正西方向,OA=200米,一部拖拉机从O出发,以5米/秒的速度沿北偏西60°方向行驶,设拖拉机噪音污染半径为125米,试问:教室A是否在噪音污染范围内?若不在,说明理由,若在,求教室A受污染的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对今年“元旦”期间销售A、B、C三种品牌的绿色鸡蛋情况进行了统计,并绘制如图所示的扇形统计图和条形统计图.根据图中信息解答下列问题:
(1)该超市“元旦”期间共销售 个绿色鸡蛋,A品牌绿色鸡蛋在扇形统计图中所对应的扇形圆心角是 度;
(2)补全条形统计图;
(3)如果该超市的另一分店在“元旦”期间共销售这三种品牌的绿色鸡蛋1500个,请你估计这个分店销售的B种品牌的绿色鸡蛋的个数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点![]() 的抛物线
的抛物线![]() 的对称轴是
的对称轴是![]() ,点
,点![]() 是抛物线与
是抛物线与![]() 轴的一个交点,点
轴的一个交点,点![]() 在
在![]() 轴上,点
轴上,点![]() 是抛物线的顶点.
是抛物线的顶点.
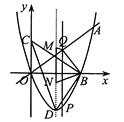

(1)求![]() 、
、![]() 的值;
的值;
(2)当![]() 是直角三角形时,求
是直角三角形时,求![]() 的面积;
的面积;
(3)设点![]() 在直线
在直线![]() 下方且在抛物线
下方且在抛物线![]() 上,点
上,点![]() 、
、![]() 在抛物线的对称轴上(点
在抛物线的对称轴上(点![]() 在点
在点![]() 的上方),且
的上方),且![]() ,过点
,过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() ,当
,当![]() 最大时,请直接写出四边形
最大时,请直接写出四边形![]() 的周长最小时点
的周长最小时点![]() 、
、![]() 、
、![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)为了掌握我市中考模拟数学试题的命题质量与难度系数,命题教师赴我市某地选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为160分)分为5组:第一组85~10;第二组100~115;第三组115~130;第四组130~145;第五组145~160,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图,观察图形的信息,回答下列问题:
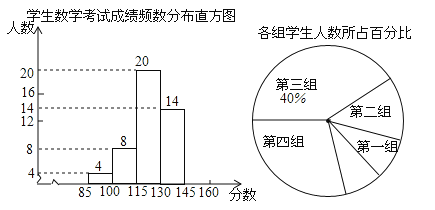
(1)本次调查共随机抽取了该年级多少名学生?并将频数分布直方图补充完整;
(2)若将得分转化为等级,规定:得分低于100分评为“D”,100~130分评为“C”,130~145分评为“B”,145~160分评为“A”,那么该年级1500名考生中,考试成绩评为“B”的学生大约有多少名?
(3)如果第一组只有一名是女生,第五组只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想,请你用列表或画树状图的方法求出所选两名学生刚好是一名女生和一名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
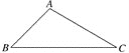
【题目】三角形中有3个角、3条边共6个元素,由其中的已知元素,求出所有未知元素的过程,叫做解三角形.
已知△ABC中,AB=![]() ,∠B=45°,BC=1+
,∠B=45°,BC=1+![]() ,解△ABC.
,解△ABC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com