
分析 (1)已知了AB的长以及∠OAB的余弦值,可过B作BD⊥x轴于D,即可求出BD和AD的长,进而可得出OD的长,由此可求出B点坐标,也就得出了C点坐标.然后用待定系数法即可求出抛物线的解析式.
(2)本题可分三种情况:
①CP∥OA,可将C点纵坐标代入抛物线的解析式中,即可求出P点坐标;然后判断CP是否与OA相等即可.如果不相等,则四边形POCA是梯形,反之则不是.
②OP∥AC,先求出直线AC的解析式,由于直线OP与直线AC平行,因此两函数的斜率相同,再根据O点坐标,可求出直线OP的解析式,然后联立抛物线的解析式即可求出P点坐标.然后判断OP是否与AC相等即可.
③AP∥OC,同②.
(3)先根据Q、R的坐标求出抛物线的解析式,然后求出N点和M点的坐标,由于抛物线的开口方向不确定,因此分两种情况,由于两种情况解法相同,以开口向上为例说明:由于三角形QNM的面积无法直接求出,因此可将其面积化为其他图形面积的和差来求.过M作MG⊥x轴于G,则三角形QNM的面积可以用梯形QNMG的面积+三角形QON的面积-三角形QMG的面积来得出.然后分别表示出三角形QNM和QNR面积,进行比较即可.
解答 解:(1)如图,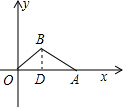
过点B作BD⊥OA于点D.
在Rt△ABD中,
∵cos∠OAB=$\frac{2\sqrt{5}}{5}$,
∴sin∠OAB=$\frac{\sqrt{5}}{5}$,
∵AB=3$\sqrt{5}$,
∴BD=AB•sin∠OAB=3$\sqrt{5}$×$\frac{\sqrt{5}}{5}$=3.
又由勾股定理,得AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=6.
∴OD=OA-AD=4.
∵点B在第一象限内,
∴点B的坐标为(4,3).
∴点B关于x轴对称的点C的坐标为(4,-3).
∵直线y=x-10与x轴交于A点,
∴点A的坐标是(10,0),
设经过O(0,0),C(4,-3),A(10,0)三点的抛物线的函数表达式为y=ax2+bx(a≠0).
由$\left\{\begin{array}{l}{16a+4b=-3}\\{100a+10b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{8}}\\{b=-\frac{5}{4}}\end{array}\right.$,
∴经过O,C,A三点的抛物线的函数表达式为y=$\frac{1}{8}$x2-$\frac{5}{4}$x;
(2)假设在(1)中的抛物线上存在点P,使以P,O,C,A为顶点的四边形为梯形.
①∵点C(4,-3)不是抛物线y=$\frac{1}{8}$x2-$\frac{5}{4}$x的顶点,
∴过点C作直线OA的平行线与抛物线交于点P1.
则直线CP1的函数表达式为y=-3.
对于y=$\frac{1}{8}$x2-$\frac{5}{4}$x,令y=-3,则x=4或x=6.
∴$\left\{\begin{array}{l}{x=4}\\{y=-3}\end{array}\right.$或$\left\{\begin{array}{l}{x=6}\\{y=-3}\end{array}\right.$.
而点C(4,-3),
∴P1(6,-3).
在四边形P1AOC中,CP1∥OA,显然CP1≠OA.
∴点P1(6,-3)是符合要求的点.
②若AP2∥CO.设直线CO的函数表达式为y=k1x.
将点C(4,-3)代入,
得4k1=-3.
∴k1=-$\frac{3}{4}$.
∴直线CO的函数表达式为y=-$\frac{3}{4}$x.
于是可设直线AP2的函数表达式为y=-$\frac{3}{4}$x+b1.
将点A(10,0)代入,
得-$\frac{3}{4}$×10+b1=0.
∴b1=7.5.
∴直线AP2的函数表达式为y=-$\frac{3}{4}$x+$\frac{15}{2}$.
由$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{y=\frac{1}{8}{x}^{2}-\frac{5}{4}x}\end{array}\right.$,
得:x2-4x-60=0,
即(x-10)(x+6)=0.
∴$\left\{\begin{array}{l}{x=10}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-6}\\{y=12}\end{array}\right.$.
而点A(10,0),
∴P2(-6,12).
过点P2作P2E⊥x轴于点E,则P2E=12.
在Rt△AP2E中,由勾股定理,
得AP2=$\sqrt{{P}_{2}{E}^{2}+A{E}^{2}}$=$\sqrt{1{2}^{2}+1{6}^{2}}$=20.
而CO=OB=5.
∴在四边形P2OCA中,AP2∥CO,但AP2≠CO.
∴点P2(-6,12)是符合要求的点.
③若OP3∥CA.设直线CA的函数表达式为y=k2x+b2.
将点A(10,0),C(4,-3)代入,
得$\left\{\begin{array}{l}{10{k}_{2}+{b}_{2}=0}\\{4{k}_{2}+{b}_{2}=-3}\end{array}\right.$.
∴直线CA的函数表达式为y=$\frac{1}{2}$x-5.
∴直线OP3的函数表达式为y=$\frac{1}{2}$x.
由$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{y=\frac{1}{8}{x}^{2}-\frac{5}{4}x}\end{array}\right.$,
得:x2-14x=0,
即x(x-14)=0.
∴$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=14}\\{y=7}\end{array}\right.$,
而点O(0,0),
∴P3(14,7).
过点P3作P3F⊥x轴于点F,则|P3F|=7.
在Rt△OP3F中,由勾股定理,
得OP3=$\sqrt{{P}_{3}{F}^{2}+O{F}^{2}}$=$\sqrt{{7}^{2}+1{4}^{2}}$=7$\sqrt{5}$.
而CA=AB=3$\sqrt{5}$.
∴在四边形P3OCA中,OP3∥CA,但|OP3|≠|CA|.
∴点P3(14,7)是符合要求的点.
综上可知,在(1)中的抛物线上存在点P1(6,-3),P2(-6,12),P3(14,7),
使以P,O,C,A为顶点的四边形为梯形.
(3)由题知,抛物线的开口可能向上,也可能向下.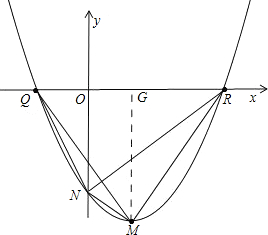
①当抛物线开口向上时,则此抛物线与y轴的负半轴交于点N.
可设抛物线的函数表达式为y=a(x+2k)(x-5k)(a>0).
即y=ax2-3akx-10ak2=a(x-1.5k)2-$\frac{49}{4}$ak2.
如图,过点M作MG⊥x轴于点G.
∵Q(-2k,0),R(5k,0),G(1.5k,0),N(0,-10ak2),M(1.5k,-$\frac{49}{4}$ak2),
∴QO=2k,QR=7k,OG=1.5k,QG=3.5k,ON=10ak2,MG=$\frac{49}{4}$ak2.
∴S△QNR=$\frac{1}{2}$QR•ON=$\frac{1}{2}$×7k×10ak2=35ak3.
S△QNM=S△QNO+S梯形ONMG-S△QMG=$\frac{1}{2}$•QO•ON+$\frac{1}{2}$(ON+GM)•OG-$\frac{1}{2}$•QG•GM=$\frac{1}{2}$×2k×10ak2+$\frac{1}{2}$×(10ak2+$\frac{49}{4}$ak2)×1.5k-$\frac{1}{2}$×3.5k×$\frac{49}{4}$ak2=$\frac{21}{4}$ak3.
∴S△QNM:S△QNR=3:20.
②当抛物线开口向下时,则此抛物线与y轴的正半轴交于点N.
同理,可得S△QNM:S△QNR=3:20.
综上可知,S△QNM:S△QNR的值为3:20.
点评 此题考查了抛物线解析式的确定、梯形的判定、三角形面积的求法等重要知识点,(2)(3)小题中,都用到了分类讨论的数学思想,难点在于考虑问题要全面,做到不重不漏.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:填空题
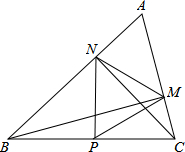 如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N.P为BC边的中点,连接PM、PN,则下列结论:①PM=PN;②$\frac{AM}{AB}=\frac{AN}{AC}$;③△PMN为等边三角形;④当△ABC=45°时,BN=PC,其中正确的是①②③.(把所有正确结论的序号都选上)
如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N.P为BC边的中点,连接PM、PN,则下列结论:①PM=PN;②$\frac{AM}{AB}=\frac{AN}{AC}$;③△PMN为等边三角形;④当△ABC=45°时,BN=PC,其中正确的是①②③.(把所有正确结论的序号都选上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
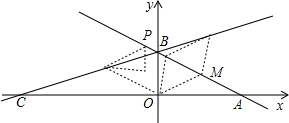 如图,直线y=kx+b的图象分别交x轴、y轴于点A,B,且OA,OB的长是方程x(6-x)=8的两个根(OA>OB),点C在x轴的负半轴上,tan∠BCA=$\frac{1}{3}$,M是AB的中点.
如图,直线y=kx+b的图象分别交x轴、y轴于点A,B,且OA,OB的长是方程x(6-x)=8的两个根(OA>OB),点C在x轴的负半轴上,tan∠BCA=$\frac{1}{3}$,M是AB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
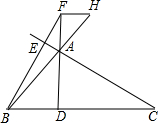 如图,在△ABC中,∠ABC=45°,∠BAC>90°,它的两条高AD,BE交于点F,过点F作FH∥BC交BA的延长线于点H,问AD,FH,CD之间有什么样的数量关系?并说明你的结论.
如图,在△ABC中,∠ABC=45°,∠BAC>90°,它的两条高AD,BE交于点F,过点F作FH∥BC交BA的延长线于点H,问AD,FH,CD之间有什么样的数量关系?并说明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com