
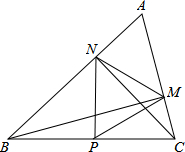
 如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N.P为BC边的中点,连接PM、PN,则下列结论:①PM=PN;②$\frac{AM}{AB}=\frac{AN}{AC}$;③△PMN为等边三角形;④当△ABC=45°时,BN=PC,其中正确的是①②③.(把所有正确结论的序号都选上)
如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N.P为BC边的中点,连接PM、PN,则下列结论:①PM=PN;②$\frac{AM}{AB}=\frac{AN}{AC}$;③△PMN为等边三角形;④当△ABC=45°时,BN=PC,其中正确的是①②③.(把所有正确结论的序号都选上) 分析 根据直角三角形斜边上的中线等于斜边的一半可判断①正确;
先证明△ABM∽△ACN,再根据相似三角形的对应边成比例可判断②正确;
先根据直角三角形两锐角互余的性质求出∠ABM=∠ACN=30°,再根据三角形的内角和定理求出∠BCN+∠CBM=60°,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BPN+∠CPM=120°,从而得到∠MPN=60°,又由①得PM=PN,根据有一个角是60°的等腰三角形是等边三角形可判断③正确;
当∠ABC=45°时,∠BCN=45°,由P为BC边的中点,得出BN=$\sqrt{2}$PB=$\sqrt{2}$PC,判断④错误.
解答 解:①∵BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,
∴PM=$\frac{1}{2}$BC,PN=$\frac{1}{2}$BC,
∴PM=PN,正确;
②在△ABM与△ACN中,
∵∠A=∠A,∠AMB=∠ANC=90°,
∴△ABM∽△ACN,
∴$\frac{AM}{AB}=\frac{AN}{AC}$;正确; ③∵∠A=60°,BM⊥AC于点M,CN⊥AB于点N,
③∵∠A=60°,BM⊥AC于点M,CN⊥AB于点N,
∴∠ABM=∠ACN=30°,
在△ABC中,∠BCN+∠CBM=180°-60°-30°×2=60°,
∵点P是BC的中点,BM⊥AC,CN⊥AB,
∴PM=PN=PB=PC,
∴∠BPN=2∠BCN,∠CPM=2∠CBM,
∴∠BPN+∠CPM=2(∠BCN+∠CBM)=2×60°=120°,
∴∠MPN=60°,
∴△PMN是等边三角形,正确;
④当∠ABC=45°时,∵CN⊥AB于点N,
∴∠BNC=90°,∠BCN=45°,
∴BN=CN,
∵P为BC边的中点,
∴PN⊥BC,△BPN为等腰直角三角形
∴BN=$\sqrt{2}$PB=$\sqrt{2}$PC,错误.
故答案为:①②③.
点评 本题主要考查了直角三角形30°角所对的直角边等于斜边的一半的性质,相似三角形、等边三角形、等腰直角三角形的判定与性质,等腰三角形三线合一的性质,仔细分析图形并熟练掌握性质是解题的关键.


科目:初中数学 来源: 题型:填空题
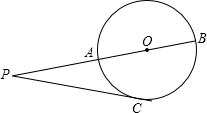 已知如图,P为⊙O外一点,过点P作⊙O的切线,切点为C,过P、Q两点作⊙O的割线交⊙O于A、B两点,且PC=4cm,PA=3cm,则⊙O的半径R=$\frac{7}{8}$cm.
已知如图,P为⊙O外一点,过点P作⊙O的切线,切点为C,过P、Q两点作⊙O的割线交⊙O于A、B两点,且PC=4cm,PA=3cm,则⊙O的半径R=$\frac{7}{8}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com