
【题目】如图,已知等边三角形△ABC,点 D,E 分别在 CA,CB 的延长线上,且 BE=CD,O为 BC 的中点,MO⊥AB 交 DE 于点 M,OM=![]() ,AD=2,则 AB=________________.
,AD=2,则 AB=________________.
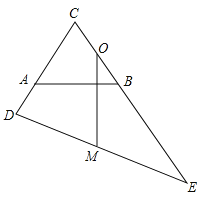
【答案】4
【解析】
先添加辅助线构造等腰三角形CFD,再推到O是EF中点,之后根据等腰三角形和等边三角形的性质来判断OM∥FD,之后判断出OM是三角形EFD的中位线即可求解本题.
解:如图,延长EC到点F,使CF=BE,
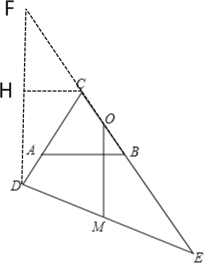
连接DF,
∵BE=CD,
∴CF=CD,
作CH⊥FD于H,
则H为FD的中点,
即FD=2FH,
∵![]() ABC是等边三角形,
ABC是等边三角形,
∴∠ACB=60°,
∴∠F=∠FDC=30°,
设![]() ABC的边长为4a,
ABC的边长为4a,
则CF=CD=2+4a,CE=4a+4a+2=8a+2,
∵O是BC中点,
∴OC=OB=2a,
∴OF=OE=6a+2,
故O为EF中点,
∵MO⊥AB 交 DE 于点 M,
∴∠BOM=30°=∠F,
∴OM∥FD,
故M为ED中点,
∴![]() ,
,
故![]() ,
,
在直角![]() CHF中,
CHF中,
∵CF=4a+2,∠F=30°,
∴CH=2a+1,
![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴AB=4a=4;
故答案为:4.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
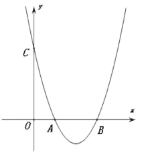
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n与x轴正半轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)利用直尺和圆规,作出抛物线y=x2+mx+n的对称轴(尺规作图,保留作图痕迹,不写作法);
(2)若△OBC是等腰直角三角形,且其腰长为3,求抛物线的解析式;
(3)在(2)的条件下,点P为抛物线对称轴上的一点,则PA+PC的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=10cm,E为对角线BD上一动点,连接AE,CE,过E点作EF⊥AE,交直线BC于点F.E点从B点出发,沿着BD方向以每秒2cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2,E点的运动时间为x秒.
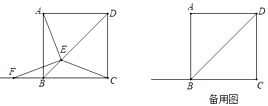
(1)求证:CE=EF;
(2)求y与x之间关系的函数表达式,并写出自变量x的取值范围;
(3)求△BEF面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月可售出500千克,销售单价每涨价1元,月销售量就减少10千克.
(1)①求出月销售量y(千克)与销售单价x(元/千克)之间的函数关系式;
②求出月销售利润w(元)与销售单价x(元/千克)之间的函数关系式;
(2)在月销售成本不超过10000元的情况下,使月销售利润达到8000元,销售单价应定为多少元?
(3)当销售单价定为多少元时,能获得最大利润?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的箱子里有四张外形相同的卡片卡片上分别标有数字﹣1,1,3,5.摸出一张后,记下数字,再放回,摇匀后再摸出一张,记下数字.以第一次得到的放字为横坐标,第二次得到的数字为纵坐标,得到一个点则这个点.恰好在直线y=﹣x+4上的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=![]() +b(a、b为常数且a≠0)中,当x=2时,y=4;当x=﹣1时,y=1.请对该函数及其图象进行如下探究:
+b(a、b为常数且a≠0)中,当x=2时,y=4;当x=﹣1时,y=1.请对该函数及其图象进行如下探究:
(1)求该函数的解析式,并直接写出该函数自变量x的取值范围;
(2)请在下列直角坐标系中画出该函数的图象;
(3)请你在上方直角坐标系中画出函数y=2x的图象,结合上述函数的图象,写出不等式![]() +b≤2x的解集.
+b≤2x的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家所在居民楼的对面有一座大厦AB,高为74米,为测量居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.
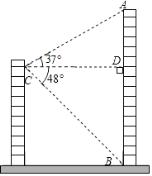
(1)求∠ACB的度数;
(2)求小明家所在居民楼与大厦之间的距离.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin48°≈
,sin48°≈![]() ,cos48°≈
,cos48°≈![]() ,tan48°≈
,tan48°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
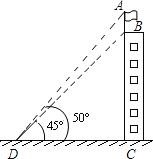
【题目】测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)
(1)若已知CD=20米,求建筑物BC的高度;
(2)若已知旗杆的高度AB=5米,求建筑物BC的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com