
【题目】某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月可售出500千克,销售单价每涨价1元,月销售量就减少10千克.
(1)①求出月销售量y(千克)与销售单价x(元/千克)之间的函数关系式;
②求出月销售利润w(元)与销售单价x(元/千克)之间的函数关系式;
(2)在月销售成本不超过10000元的情况下,使月销售利润达到8000元,销售单价应定为多少元?
(3)当销售单价定为多少元时,能获得最大利润?最大利润是多少元?
【答案】(1)①y=﹣10x+1000;②w=﹣10x2+1400x﹣40000;(2)不超过10000元的情况下,使月销售利润达到8000元,销售单价应定为80元;(3)售价定为70元时会获得最大利润,最大利润是9000元
【解析】
(1)根据题意可以得到月销售利润w(单位:元) 与售价x(单位:元/千克)之间的函数解析式;
(2)根据题意可以得到方程和相应的不等式,从而可以解答本题;
(3)根据(1)中的关系式化为顶点式即可解答本题.
解:(1)①由题意可得:y=500﹣(x﹣50)×10=﹣10x+1000;
②w=(x﹣40)[﹣10x+1000]=﹣10x2+1400x﹣40000;
(2)设销售单价为a元,
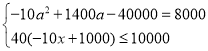 ,
,
解得,a=80,
答:商店想在月销售成本不超过10000元的情况下,使月销售利润达到8000元,销售单价应定为80元;
(3)∵y=﹣10x2+1400x﹣40000=﹣10(x﹣70)2+9000,
∴当x=70时,y取得最大值,此时y=9000,
答:当售价定为70元时会获得最大利润,最大利润是9000元;


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】下表是二次函数y=ax2+bx+c的x,y的部分对应值:
x | … | - | 0 |
| 1 |
| 2 |
| … |
y | … |
| -1 | - | m | - | -1 | n | … |
则对于该函数的性质的判断:
①该二次函数有最大值;②不等式y>-1的解集是x<0或x>2;
③方程ax2+bx+c=0的两个实数根分别位于-![]() <x<0和2<x<
<x<0和2<x<![]() 之间;
之间;
④当x>0时,函数值y随x的增大而增大;
其中正确的是:
A.②③B.②④C.①③D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
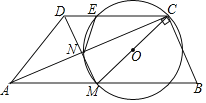
【题目】如图,在Rt△ABC中,M是斜边AB的中点,以CM为直径作圆O交AC于点N,延长MN至D,使ND=MN,连接AD、CD,CD交圆O于点E.
(1)判断四边形AMCD的形状,并说明理由;
(2)求证:ND=NE;
(3)若DE=2,EC=3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
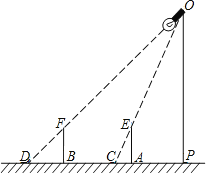
【题目】如图,学校操场旁立着一杆路灯(线段OP).小明拿着一根长2m的竹竿去测量路灯的高度,他走到路灯旁的一个地点A竖起竹竿(线段AE),这时他量了一下竹竿的影长AC正好是1m,他沿着影子的方向走了4m到达点B,又竖起竹竿(线段BF),这时竹竿的影长BD正好是2m,请利用上述条件求出路灯的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:其中,正确的个数有( )
①b2﹣4ac<0;②a﹣b+c<0;③abc>0;④m>﹣2.
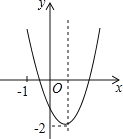
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边三角形△ABC,点 D,E 分别在 CA,CB 的延长线上,且 BE=CD,O为 BC 的中点,MO⊥AB 交 DE 于点 M,OM=![]() ,AD=2,则 AB=________________.
,AD=2,则 AB=________________.
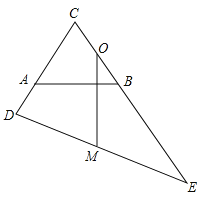
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个阳光明媚的上午,小明和小兰相约从鲁能巴蜀中学沿相同的路线去龙头寺公园写生,小明出发5分钟后小兰才出发,此时小明发现忘记带颜料,立即按原速原路回学校拿颜料,小明拿到颜料后,以比原速提髙20%的速度赶去公园,结果还是比小兰晚2分钟到公园(小明拿颜料的时间忽略不计).在整个过程中,小兰保持匀速运动,小明提速前后也分别保持匀速运动,如图所示是小明与小兰之间的距离![]() (米)与小明出发的时间
(米)与小明出发的时间![]() (分钟)之间的函数图象,则学校到公园的距离为_______米.
(分钟)之间的函数图象,则学校到公园的距离为_______米.
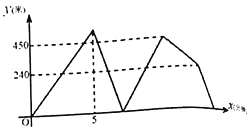
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠EFC′=120°,那么∠ABE的度数为__________。
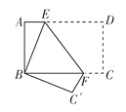
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校准备近期做一个关于新冠肺炎的专刊学生手抄报,想知道同学们对新冠肺炎知识的了解程度,决定随机抽取部分同学进行次问卷调查,并根据收集到的信息进行了统计,绘制了下面两.幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的同学共有 名;
(2)请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小;
(3)为了让全校师生都能更好地预防新冠肺炎,学生会准备组织一次宣讲活动,由问卷调查中“了解”的几名同学组成一个宣讲团,已知这几名同学中只有两个女生,若要在该宣讲团中任选两名同学在全校师生大会上作代表发言,请用列表或画树状图的方法,求选取的两名同学都是女生的概率.
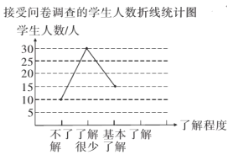

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com