
【题目】下表是二次函数y=ax2+bx+c的x,y的部分对应值:
x | … | - | 0 |
| 1 |
| 2 |
| … |
y | … |
| -1 | - | m | - | -1 | n | … |
则对于该函数的性质的判断:
①该二次函数有最大值;②不等式y>-1的解集是x<0或x>2;
③方程ax2+bx+c=0的两个实数根分别位于-![]() <x<0和2<x<
<x<0和2<x<![]() 之间;
之间;
④当x>0时,函数值y随x的增大而增大;
其中正确的是:
A.②③B.②④C.①③D.①④
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴相交于点
轴相交于点![]() ,与反比例函数
,与反比例函数![]() 的图象相交于点
的图象相交于点![]() ,
,![]() .
.
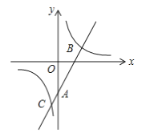
(1)求一次函数和反比例函数的解析式;
(2)根据图象,直接写出![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为等腰三角形,如果存在,请求点
为等腰三角形,如果存在,请求点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 中,AB=8,BC=6,将矩形 ABCD 绕点 A 逆时针旋转得到矩形 AEFG,AE,FG 分别交射线CD 于点 PH,连结 AH,若 P 是 CH 的中点,则△APH 的周长为( )
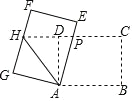
A. 15 B. 18 C. 20 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的是_____(填序号).
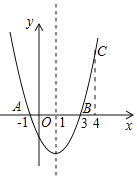
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n与x轴正半轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)利用直尺和圆规,作出抛物线y=x2+mx+n的对称轴(尺规作图,保留作图痕迹,不写作法);
(2)若△OBC是等腰直角三角形,且其腰长为3,求抛物线的解析式;
(3)在(2)的条件下,点P为抛物线对称轴上的一点,则PA+PC的最小值为 .
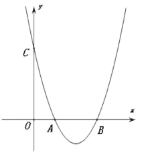
查看答案和解析>>
科目:初中数学 来源: 题型:
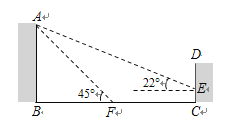
【题目】(满分8分)如图,某教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45°时,教学楼顶A在地面上的影子F与墙角C的距离为18m (B、F、C在一条直线上).
求教学楼AB的高度.(结果保留整数)
(参考数据:sin22°![]() 0.37,cos22°
0.37,cos22°![]() 0.93,tan22°
0.93,tan22°![]() 0.40 .)
0.40 .)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月可售出500千克,销售单价每涨价1元,月销售量就减少10千克.
(1)①求出月销售量y(千克)与销售单价x(元/千克)之间的函数关系式;
②求出月销售利润w(元)与销售单价x(元/千克)之间的函数关系式;
(2)在月销售成本不超过10000元的情况下,使月销售利润达到8000元,销售单价应定为多少元?
(3)当销售单价定为多少元时,能获得最大利润?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com