
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴相交于点
轴相交于点![]() ,与反比例函数
,与反比例函数![]() 的图象相交于点
的图象相交于点![]() ,
,![]() .
.
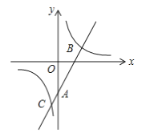
(1)求一次函数和反比例函数的解析式;
(2)根据图象,直接写出![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为等腰三角形,如果存在,请求点
为等腰三角形,如果存在,请求点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【答案】(1)![]() ;
; ![]() ;(2)
;(2)![]() 或
或![]() ;(3)存在,
;(3)存在,![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用待定系数法求出反比例函数解析式,进而求出点C坐标,最后用再用待定系数法求出一次函数解析式;
(2)利用图象直接得出结论;
(3)分![]() 、
、![]() 、
、![]() 三种情况讨论,即可得出结论.
三种情况讨论,即可得出结论.
(1)![]() 一次函数
一次函数![]() 与反比例函数
与反比例函数![]() ,相交于点
,相交于点![]() ,
,![]() ,
,
∴把![]() 代入
代入![]() 得:
得:![]() ,
,
∴![]() ,
,
∴反比例函数解析式为![]() ,
,
把![]() 代入
代入![]() 得:
得:![]() ,
,
∴![]() ,
,
∴点C的坐标为![]() ,
,
把![]() ,
,![]() 代入
代入![]() 得:
得:![]() ,
,
解得:![]() ,
,
∴一次函数解析式为![]() ;
;
(2)根据函数图像可知:
当![]() 或
或![]() 时,一次函数的图象在反比例函数图象的上方,
时,一次函数的图象在反比例函数图象的上方,
∴当![]() 或
或![]() 时,
时,![]() ;
;
(3)存在![]() 或
或![]() 或
或![]() 或
或![]() 时,
时,![]() 为等腰三角形,理由如下:
为等腰三角形,理由如下:
过![]() 作
作![]() 轴,交
轴,交![]() 轴于
轴于![]() ,
,
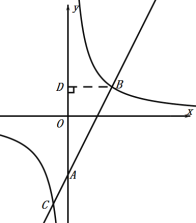
∵直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
∴令![]() 得,
得,![]() ,
,
∴点A的坐标为![]() ,
,
∵点B的坐标为![]() ,
,
∴点D的坐标为![]() ,
,
∴![]()
![]()
![]() ,
,
①当![]() 时,则
时,则![]() ,
,
![]() ,
,
∴点P的坐标为:![]() 、
、![]() ;
;
②当![]() 时,
时,
![]() 是等腰三角形,
是等腰三角形,![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
∵点D的坐标为![]() ,
,
∴点P的坐标为![]() ,即
,即![]() ;
;
③当![]() 时,如图:
时,如图:
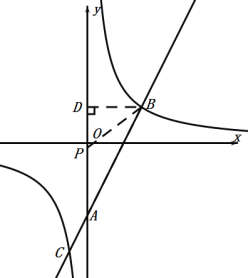
设![]() ,
,
则![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() 由勾股定理得:
由勾股定理得:
![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() ,
,
∴点P的坐标为![]() ,即
,即![]() ,
,
综上所述,当![]() 或
或![]() 或
或![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过点A(-1,0)和点B(4,0),且与y轴交于点C,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点,连接CA,CD,PD,PB.
⑴求抛物线的解析式;
⑵当△PDB的面积等于△CAD的面积时,求点P的坐标;
⑶当m>0,n>0时,过点P作直线PE⊥y轴于点E交直线BC于点F,过点F作FG⊥x轴于点G,连接EG,请直接写出随着点P的运动,线段EG的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年12月5日,备受关注的郑州奥体中心“一场两馆”主体结构已完成,装饰装修完成![]() ,据了解,郑州奥体中心将作为2019年在郑州市举办的第十一届全国少数民族传统体自运动会主办场地,包括“一场两馆”,即
,据了解,郑州奥体中心将作为2019年在郑州市举办的第十一届全国少数民族传统体自运动会主办场地,包括“一场两馆”,即![]() 万个座位的体育场、
万个座位的体育场、![]() 万个座位的体育馆和
万个座位的体育馆和![]() 和座位的游泳馆,图1是装饰现场一辆吊车的实物图,图2是其工作示意图,
和座位的游泳馆,图1是装饰现场一辆吊车的实物图,图2是其工作示意图,![]() 是可以伸缩的起重臂,其转动点
是可以伸缩的起重臂,其转动点![]() 离地面
离地面![]() 的高度
的高度![]() 为
为![]() 当起重臂
当起重臂![]() 长度为
长度为![]() ,张角
,张角![]() 为
为![]() 时,求操作平台
时,求操作平台![]() 离地面的高度(结果保留小数点后一位参考数据:
离地面的高度(结果保留小数点后一位参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
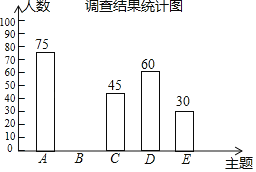
【题目】2019年3月19日,河南省教育厅发布《关于推进中小学生研学旅行的实施方案》,某中学为落实方案,给学生提供了以下五种主题式研学线路:A.“红色河南”,B.“厚重河南”C.“出彩河南”,D.“生态河南”,E.“老家河南”为了解学生最喜欢哪一种研学线路(每人只选取一种),随机抽取了部分学生进行调查,将调查结果绘制成如下不完整的统计表和统计图.根据以上信息解答下列问题:
调查结果统计表
主题 | 人数/人 | 百分比 |
A | 75 | n% |
B | m | 30% |
C | 45 | 15% |
D | 60 | |
E | 30 |
(1)本次接受调查的总人数为 人,统计表中m= ,n= .
(2)补全条形统计图.
(3)若把条形统计图改为扇形统计图,则“生态河南”主题线路所在扇形的圆心角度是 .
(4)若该实验中学共有学生3000人,请据此估计该校最喜欢“老家河南”主题线路的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的两条邻边长分别为6和8,则第n个菱形的周长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且AC在直线l上,将△ABC绕点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+![]() ;…按此规律继续旋转,直到点P2020为止,则AP2020等于_______.
;…按此规律继续旋转,直到点P2020为止,则AP2020等于_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
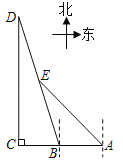
【题目】如图,为某景区五个景点A、B、C、D、E的平面示意图,B、A在C的正东方向,D在C的正北方向,D和E均在B的北偏西18°方向上,E在A的西北方向上,C、D相距1000米,E在BD的中点处,求景点B、A之间的距离.(结果保留整数)
(参考数据:sin18°≈0.3;cos18°≈0.9;tan18°≈0.3;sin72°≈0.9;cos72°≈0.3;tan72°≈3.1;![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是二次函数y=ax2+bx+c的x,y的部分对应值:
x | … | - | 0 |
| 1 |
| 2 |
| … |
y | … |
| -1 | - | m | - | -1 | n | … |
则对于该函数的性质的判断:
①该二次函数有最大值;②不等式y>-1的解集是x<0或x>2;
③方程ax2+bx+c=0的两个实数根分别位于-![]() <x<0和2<x<
<x<0和2<x<![]() 之间;
之间;
④当x>0时,函数值y随x的增大而增大;
其中正确的是:
A.②③B.②④C.①③D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com